Предмет: Математика,
автор: MrBabyin
Можете ,будь ласка, дати розгорнуту відповідь
Приложения:
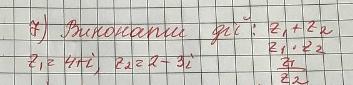
Ответы
Автор ответа:
1
Ответ:
Даны комплексные числа : .
Найдём сумму комплексных чисел .
Найдём произведение комплексных чисел , применяя формулу
.
Найдём частное комплексных чисел
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: koljabychenko012
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: balladofreedom
Предмет: Алгебра,
автор: sashatym03