Предмет: Математика,
автор: MrBabyin
Можете ,будь ласка, дати розгорнуту відповідь
Приложения:
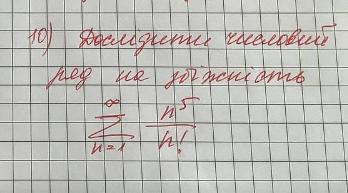
Ответы
Автор ответа:
1
Решение.
Исследовать ряд на сходимость .
Применим к знакоположительному ряду достаточный признак сходимости Даламбера .
Так как 0 < 1 , то ряд сходится .
Приложения:
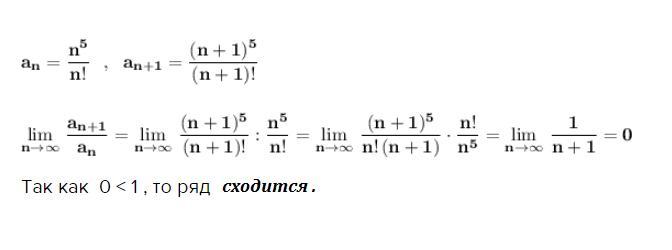
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: balladofreedom
Предмет: Алгебра,
автор: daniil1835
Предмет: Физика,
автор: sbjsjdhdj
Предмет: Алгебра,
автор: sashatym03