Предмет: Алгебра,
автор: sw3toff
Даю 100 баллов. Розв’язати рівняння Бернуллі
Приложения:
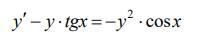
Ответы
Автор ответа:
1
Данное уравнение - это уравнение Бернулли. Поделим всё на и сделаем замену
Замена
Тогда, наше уравнение можно переписать
Снова делаем замену , тогда
Решаем первое уравнение
Решаем второе уравнение
Делаем обратную замену
Похожие вопросы
Предмет: Українська мова,
автор: angelinass1515
Предмет: Українська мова,
автор: fashiongame111
Предмет: Українська мова,
автор: dumpisner
Предмет: Математика,
автор: Daeir
Предмет: Химия,
автор: 7AMG77