Question

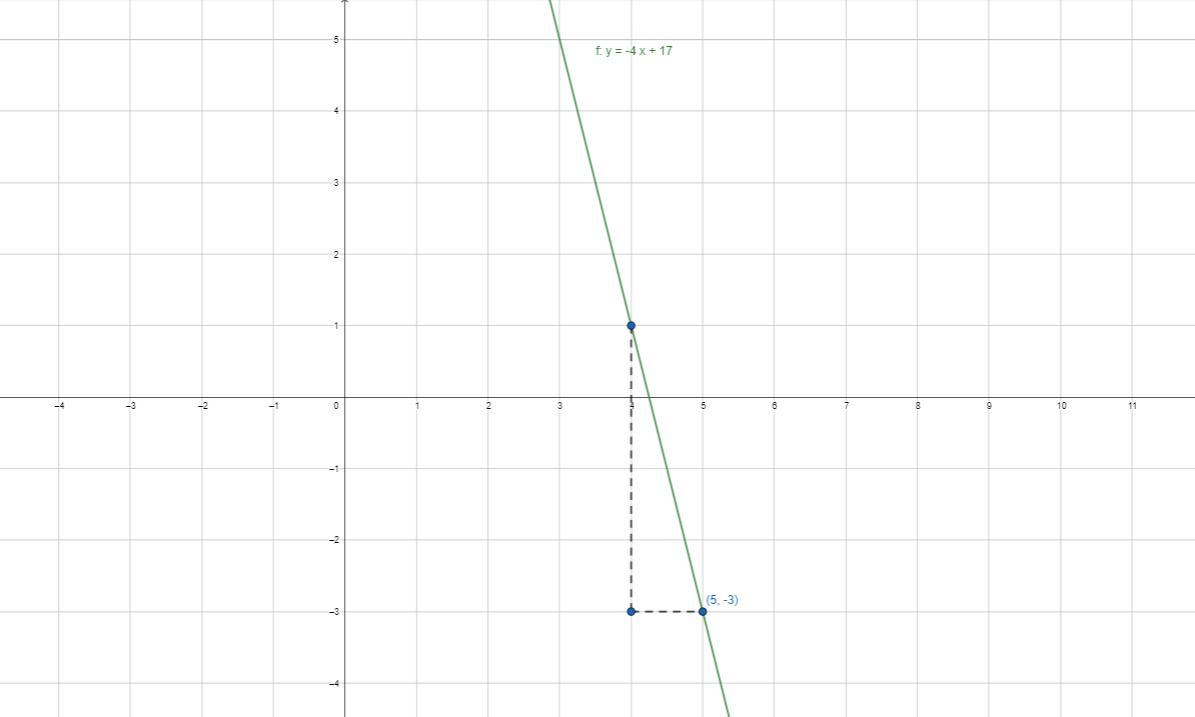
Найдите уравнение прямой, проходящей через точку
(х, у) = (5, −3) и имеет наклон −4.

Answer 1

Ответ:

$y=-4x+17$.

Объяснение:

$y=mx+b$

Дано: $m=-4$ (наклон -4).

$(x-x_0)\cdot m=y-y_0\\(5;-3)\\\\(x-5)\cdot(-4)=y-(-3)\\-4x+20=y+3\\y=-4x+20-3\\y=-4x+17$

Answer 2

Ответ:

y  = -4x + 17

Объяснение:

y = kx + b

Наша прямая проходит через точку ( 5 ;  -3)  ,  нам также известно что ее угловой коэффициент равен     k  = -4

Тогда :

y = -4x + b

Подставим координаты ( 5 ;  -3)

-4·5 + b =  - 3

-20 + b = -3

b = 17

Тогда уравнение нашей прямой будет иметь вид :

y  =  -4x + 17