Question

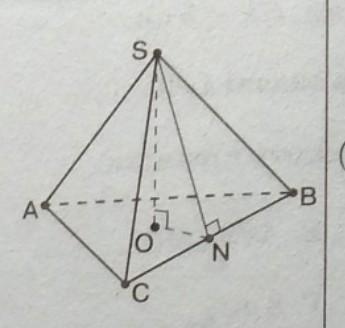
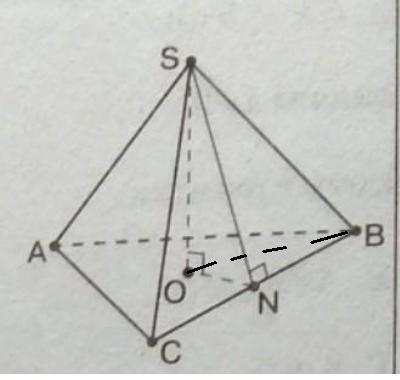
SABC-правильна трикутна піраміда
SB=3√13 см,SO=3 см.
Знайдіть сторону основи піраміди.
(З розв'язком)​

Answer 1

Ответ:

Cторона основания пирамиды  равна 18 см.

Пошаговое объяснение:

Дана  правильная пирамида  SАВС , SB =3√13 cм , SO =3 cм . Найти сторону  основания пирамиды.

Рассмотрим Δ SОВ - прямоугольный, так как SО - высота .

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$SB^{2} =SO^{2} +OB^{2} ;\\OB^{2} =SB^{2} -SO^{2};\\OB= \sqrt{SB^{2} -SO^{2}} ;\\OB= \sqrt{(3\sqrt{13})^{2} -3^{2} } =\sqrt{9\cdot13 -9 } =\sqrt{9\cdot(13-1)} =\sqrt{9\cdot12 }=\sqrt{9\cdot4\cdot3 } =\\=6\sqrt{3}$

OB= 6√3 см.

Так как по условию пирамида правильная , то ОВ - радиус окружности, описанной около ΔАВС .

$R =6\sqrt3{}$ см

ΔАВС - правильный.

Для правильного треугольника

$R = \dfrac{a}{\sqrt{3} },$

где  a - сторона треугольника .

Тогда $a= R\sqrt{3}$

$a = 6\sqrt{3} \cdot \sqrt{3} =6\cdot 3 =18$ см.

Значит, cторона основания пирамиды  равна 18 см.

#SPJ1