Предмет: Алгебра,
автор: Аноним
используя формулы сложения для тангенса и котангенса, найдите значения(делать то, что я обвел карандашем кружочком)
Приложения:
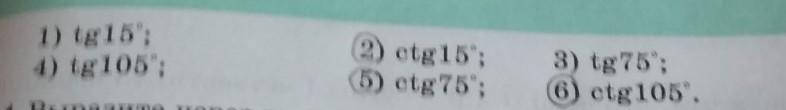
Ответы
Автор ответа:
6
Ответ:
Похожие вопросы
Предмет: Физика,
автор: Michael0101
Предмет: Химия,
автор: leonleviano
Предмет: Алгебра,
автор: keef75
Предмет: Математика,
автор: ustverap46ucz
Предмет: Математика,
автор: Nade4ka1993