Предмет: Математика,
автор: masmaks13
Найти производные функций, можно только всё подробно, с объяснением
Приложения:
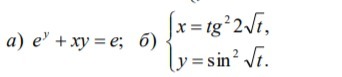
masmaks13:
можешь пожалуйста сделать и фото отправить?
пж, а то не получается и всё
ну под б ,ты можешь в инете забить решение
под а) я не знаю как выразить "у"из под экспоненты чтобы потом привести подобные
его только через логарифм можно вроде бы выразить
а в пределах разбираешься?
смотря какие
у меня был вопрос по пределам
любой в принципе предел можно решить по правилу лапиталя
там 2 пункта: в и г , пункт в нельзя лапиталем делать, а г можно
Ответы
Автор ответа:
1
1) Так как из заданного равенства выразить "у" невозможно, то найдём производную неявно заданной функции, учитывая, что "у" - функция, то есть у=у(х).
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: miaiwiw6
Предмет: Математика,
автор: elmiramuxtarova42
Предмет: Информатика,
автор: МикаКудо
Предмет: История,
автор: julburmistrova