Предмет: Геометрия,
автор: pvmnts
основания равнобедренной трапеции равны 12 см и 18 см диагональ 17 см Найдите площадь трапеции. Срочно, завтра контр
Ответы
Автор ответа:
62
Ответ: 120 см²
Объяснение:
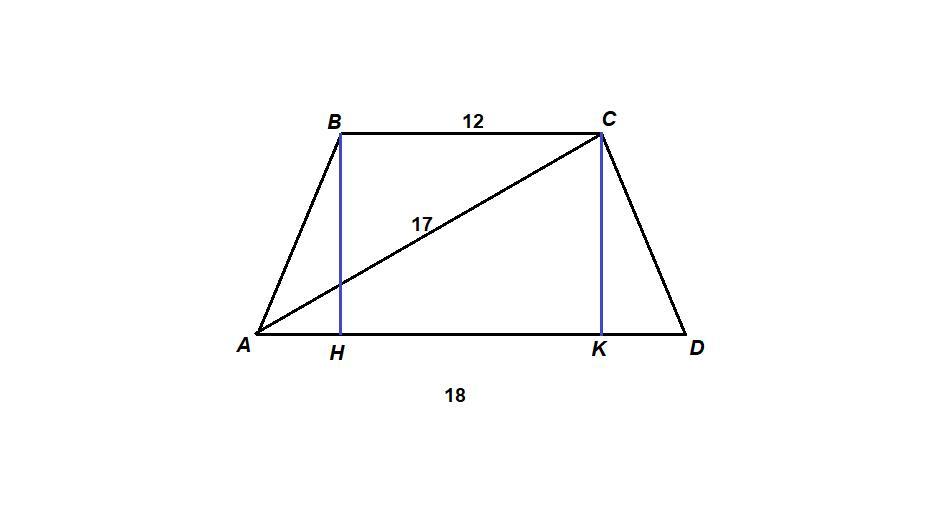
Проведем высоты ВН и СК. ВНКС - прямоугольник, так как все его углы прямые.
НК = ВС = 12 см.
ΔАВН = ΔDCK по гипотенузе и катету (∠ВНА = ∠CKD = 90°, АВ = CD как боковые стороны равнобедренной трапеции, ВН = СК как высоты), ⇒
АН = КD = (AD - КН) / 2 = (18 - 12) / 2 = 3 см
АК = АН + НК = 3 + 12 = 15 см
ΔACК: ∠AКC = 90°, по теореме Пифагора
СК = √(АС² - АК²) = √(17² - 15²) = √(289 - 225) = √64 = 8 см
Sabcd = (AD + BC)/2 · CK = (18 + 12)/2 · 8 = 120 см²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: lgabor09
Предмет: История,
автор: NagitoKomaedaa
Предмет: Математика,
автор: esbolsunnurbol
Предмет: Физика,
автор: BIOLOGIST102938