Предмет: Математика,
автор: plinda9941
найдите сумму корней уравнения
Приложения:
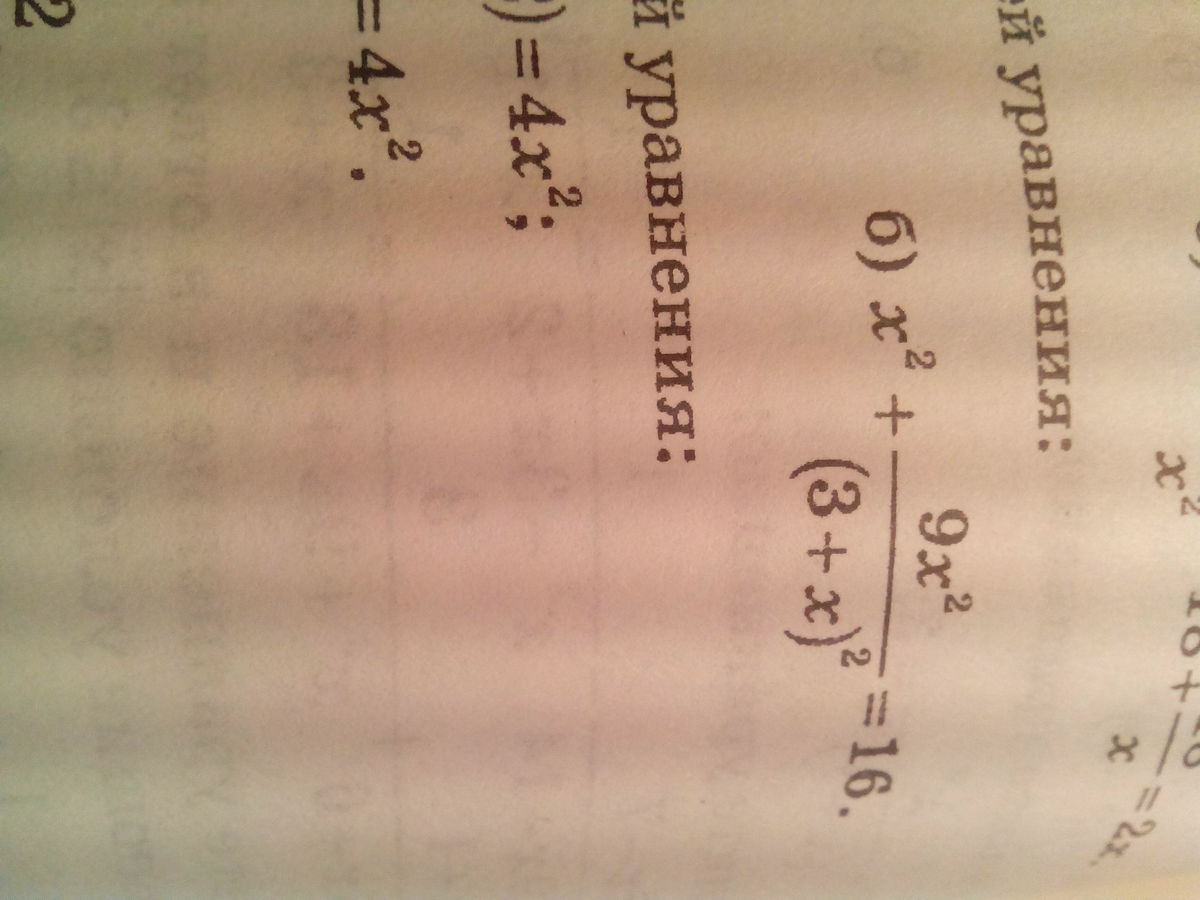
Ответы
Автор ответа:
0
Пусть x²=A, x+3=B, тогда имеем.
Возвращаемся к замене
Сумма корней:
Ответ: 2.
Автор ответа:
0
круто!"':;"";:!!!!!!
Автор ответа:
0
спасибо большее, ты гений!
Автор ответа:
0
И правда,гений )
Похожие вопросы
Предмет: Физкультура и спорт,
автор: zavyalov09090958
Предмет: Математика,
автор: mamzi6
Предмет: Математика,
автор: jopababuina
Предмет: Геометрия,
автор: atv200u
Предмет: Алгебра,
автор: maxefimenko