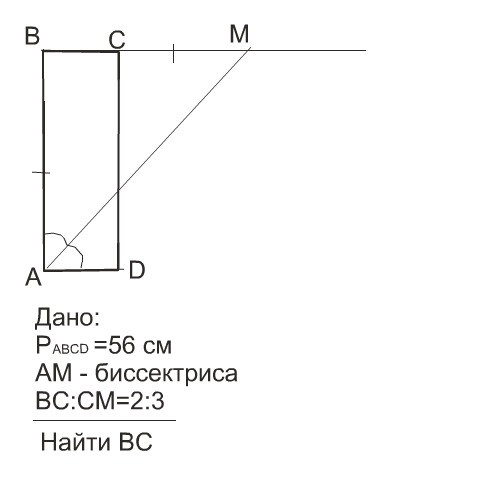
В прямоугольнике ABCD проведена биссектриса угла A, которая пересекает сторону BC в точке M, причем BC:MC=2:3. Найдите BC, если периметр ABCD равен 56 см.
Ответы
Дан прямоугольник ABCD
AM - биссектриса
BC/MC=2/3
P=56 см
Найти BC
Решение.
P=2*(a+b)
Так как AM биссектриса, то треугольник ABM равнобедренный. AB=BM.
BC/MC=2/3 ⇒ MC=3BM/2
Подставляем в формулу периметра:
2*(2BM+3BM/2)=56
4BM+3BM=56
7BM=56
BM=8 см
MC=3BM/2=3*8/2= 12 см
BC=BM+MC=12+8 = 20 см
Ответ. BC = 20 см
У этой задачи есть и другой вариант решения. Поскольку отношение ВС:МС=2:3, логично предположить, что МС > ВС и точка М лежит на продолжении ВС.
Обозначим коэффициент отношения ВС и МС как х.
Тогда ВС=2х, СМ=3х
Так как биссектрисой и сторонами АВ и ВМ образован равнобедренный треугольник, сторона АВ=ВМ и равна 2х+3х=5х
Р АВСD=(2х+5х)·2=56 см
(2х+5х)·2=56
14х=56
х=4
Сторона ВС =2·4=8 см
Сторона АВ=5·4=20 см
СМ=3·4=12
Проверка:
ВС:СМ=8:12=2:3