Предмет: Геометрия,
автор: tirelessly
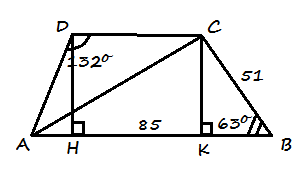
AB и CD основания трапеции, угол ABC=63◦ угол CDA=132◦ AB=85mm
BC = 51 mm. Вычислить AD, CD и диагональ AC
Ответы
Автор ответа:
0
CA можно найти по теореме косинусов:

Проведем высоту СК. С ΔСКВ можно найти СК:

DH - вторая высота в трапеции.

C ΔADH найдем AD:

Сторона DC=AB-KB-AH.
Найдем AH с ΔADH:

KB можно найти с ΔКСВ:

Получаем:

Проведем высоту СК. С ΔСКВ можно найти СК:
DH - вторая высота в трапеции.
C ΔADH найдем AD:
Сторона DC=AB-KB-AH.
Найдем AH с ΔADH:
KB можно найти с ΔКСВ:
Получаем:
Приложения:


Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Геометрия,
автор: vikavika01082006
Предмет: Английский язык,
автор: bahtiyormirzaraimov
Предмет: Алгебра,
автор: Nursaya
Предмет: Литература,
автор: Vitaha2001