Предмет: Геометрия,
автор: Ася0598
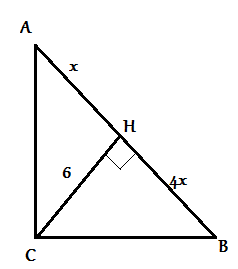
Высота прямоугольного треугольника, проведенная к гипотенузе, равна 6 см и делит гипотенузу на отрезки, длины которых относятся как 4:1. Найдите гипотенузу.
Ответы
Автор ответа:
0
Пусть АН = х см, ВН = 4х см. По свойству высоты деление гипотенузы:
Гипотенуза АВ = х +4х = 5х см.
 см
см
 см.
см.
С прямоугольного треугольника СНА.

Т.е. Катеты будут 3√5 см и 6√5 см, а гипотенуза 15 см.
Ответ: АВ = 15 см.
Гипотенуза АВ = х +4х = 5х см.
С прямоугольного треугольника СНА.
Т.е. Катеты будут 3√5 см и 6√5 см, а гипотенуза 15 см.
Ответ: АВ = 15 см.
Приложения:
Похожие вопросы
Предмет: Астрономия,
автор: alloallo3202
Предмет: Русский язык,
автор: volckows1
Предмет: Математика,
автор: hdhdhsgsh
Предмет: Математика,
автор: nikolai500