Предмет: Алгебра,
автор: Аноним
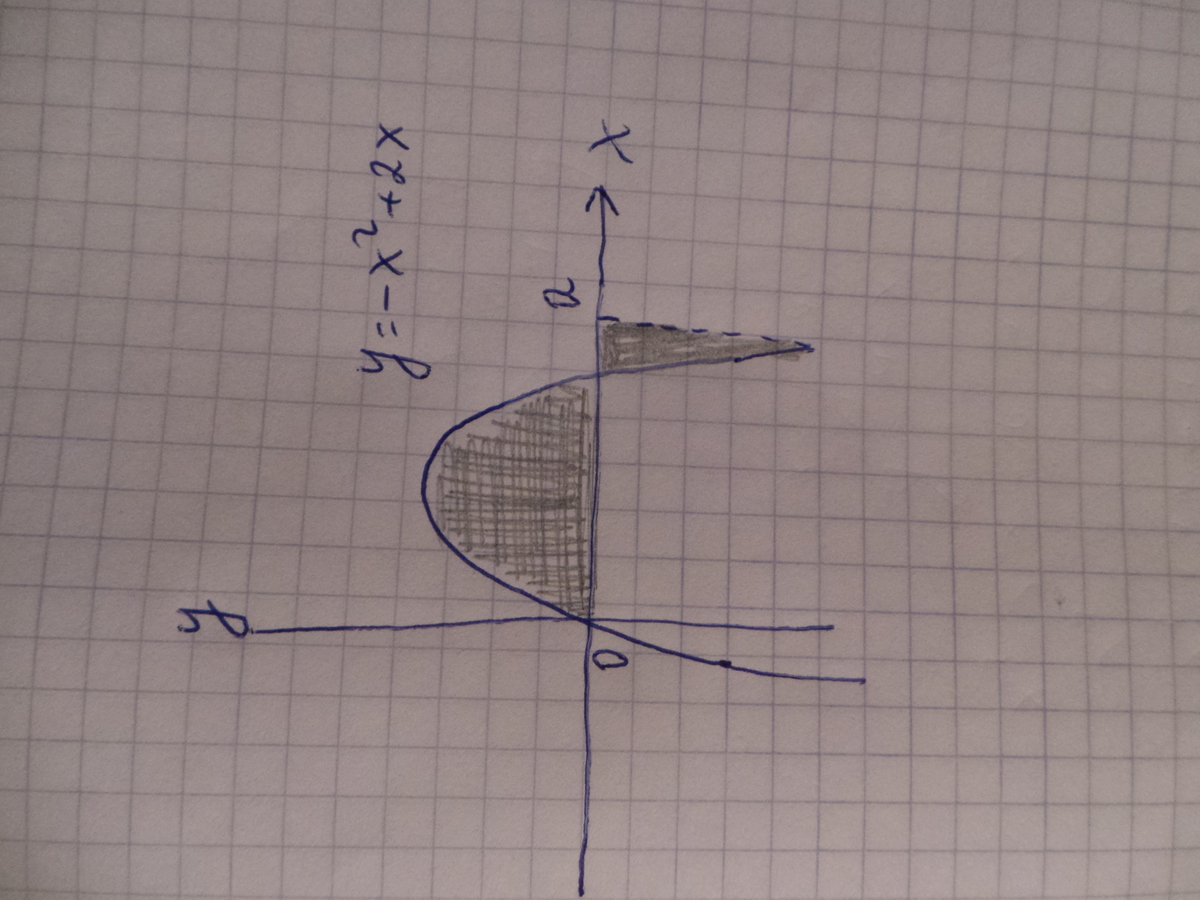
Найти а, если сумма площадей заштрихованных на графике частей равна 2 целые 2/3
Приложения:
Ответы
Автор ответа:
0
Поняла, где ошиблась, из-за чего у меня не выходил ответ :)
Суммарная площадь равна: S=S1+S2=8/3
Найдем точки пересечения параболы с осью Ох:

 - это пределы интегрирования
- это пределы интегрирования
 - площадь первой фигуры
- площадь первой фигуры
 - площадь второй фигуры
- площадь второй фигуры




 - посторонний корень
- посторонний корень
 - корень
- корень
Ответ: a=3
Суммарная площадь равна: S=S1+S2=8/3
Найдем точки пересечения параболы с осью Ох:
Ответ: a=3
Автор ответа:
0
площадь большей заштрихованной равен
Значит второй
Похожие вопросы
Предмет: История,
автор: hfhfjfjfjfjdid
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: i4752647
Предмет: Физика,
автор: Аноним
Предмет: Алгебра,
автор: katyap11