Предмет: Математика,
автор: bastrvika
помогите с решением интегралов
Приложения:
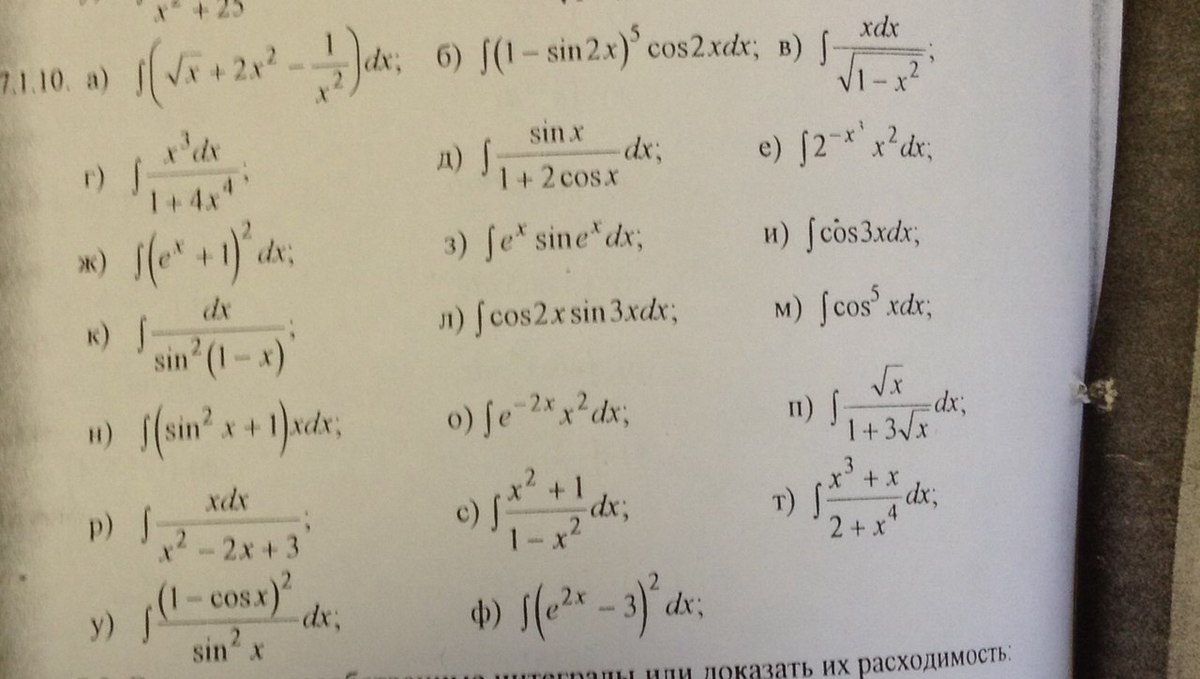
Ответы
Автор ответа:
0
Автор ответа:
0
Спасибо за помощь!! Благодаря тебе я получу автомат))
Похожие вопросы
Предмет: Алгебра,
автор: veronika0807veronika
Предмет: Английский язык,
автор: Danilasambo2007
Предмет: Українська мова,
автор: Irhaaroslav
Предмет: География,
автор: koshkaritty