Предмет: Геометрия,
автор: qwert66
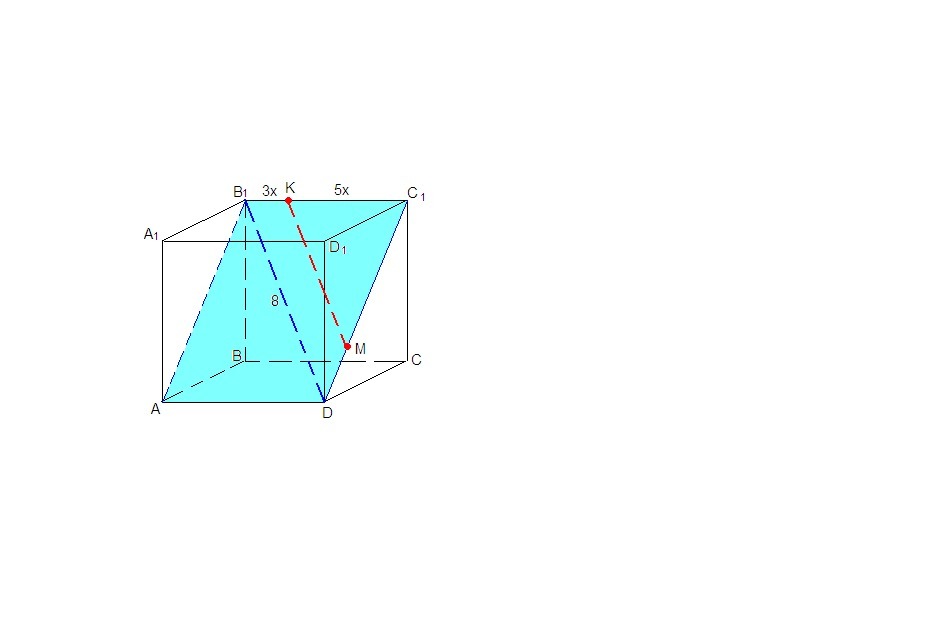
Дан куб ABCDA1B1C1D1. Диагональ B1D которого равна 8. Точка К делит ребро B1C1 в отношении 3:5, считая от B1. Через точку К проведена прямая параллельно прямой B1d. Найдите длину отрезка этой прямой, заключенной внутри куба.
Ответы
Автор ответа:
0
Построим сечение куба такой плоскостью, в которой лежала бы диагональ B₁D и точка К.
Это сечение АВ₁С₁D.
Теперь через точку К проведем прямую, параллельную B₁D. Она пересечет грань CC₁D₁D в точке М, лежащей на прямой C₁D.
КМ - искомый отрезок.
ΔС₁КМ подобен ΔС₁В₁D по двум углам (∠С₁ общий, ∠С₁КМ = ∠С₁В₁D как соответственные при пересечении КМ║В₁D секущей В₁С₁)
КМ : В₁D = С₁К : С₁В₁
КМ : 8 = 5 : 8
КМ = 5
Это сечение АВ₁С₁D.
Теперь через точку К проведем прямую, параллельную B₁D. Она пересечет грань CC₁D₁D в точке М, лежащей на прямой C₁D.
КМ - искомый отрезок.
ΔС₁КМ подобен ΔС₁В₁D по двум углам (∠С₁ общий, ∠С₁КМ = ∠С₁В₁D как соответственные при пересечении КМ║В₁D секущей В₁С₁)
КМ : В₁D = С₁К : С₁В₁
КМ : 8 = 5 : 8
КМ = 5
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Vanya0992
Предмет: Другие предметы,
автор: karolinabarvina13
Предмет: Українська мова,
автор: K1NORI
Предмет: Физика,
автор: stalkar184
Предмет: Математика,
автор: fearyt98