Предмет: Математика,
автор: Lina1com
Исследовать
сходимость ряда.
Приложения:
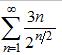
Ответы
Автор ответа:
0
применим признак Даламбера
D<1, значит сх-ся
Автор ответа:
0
1/√2<1 => ряд сходится по признаку Коши
Похожие вопросы
Предмет: Физика,
автор: fadolgopolov
Предмет: Английский язык,
автор: mstepanuk
Предмет: Қазақ тiлi,
автор: TezKerek
Предмет: Химия,
автор: vitokb
Предмет: Обществознание,
автор: serafima404