В равнобедренной трапеции диагонали являются биссектрисами острых углов. Определите периметр трапеции, если диагональ делит среднюю линию на части 8см и 12см.
1) 96 см
2) 72 см
3) 80 см
4) другой ответ
Ответы
равнобедренная трапеция - боковые стороны равны. отметим трапецию как АВСД
проведем среднюю линию МН..затем диагональ АС..она будет делить ср.линию МН на отрезки 8 и 12..и будет пересекать ее в точке О.тогда отрезок МО будет средней линией для треугольника АВС..а отрезок ОН будет среднй линией треугольника СДА
отсюда..верхнее основание = 16, а нижнее 24 .
т.к диагональ есть биссектриса..то она делит угол пополам..точнее наш угол A при основании..отсюда..угол A/2 из треугольника СДА будет равен углу Ф из треугольника АВС..Ф = А/2
отсюда А/2 также является углом в треугольнике АВС..получается АВС равнобедренный треугольник..отсюда АВ = ВС, AB = 16
значит периметр = 24 + 16 + 16 + 16 = 72 см
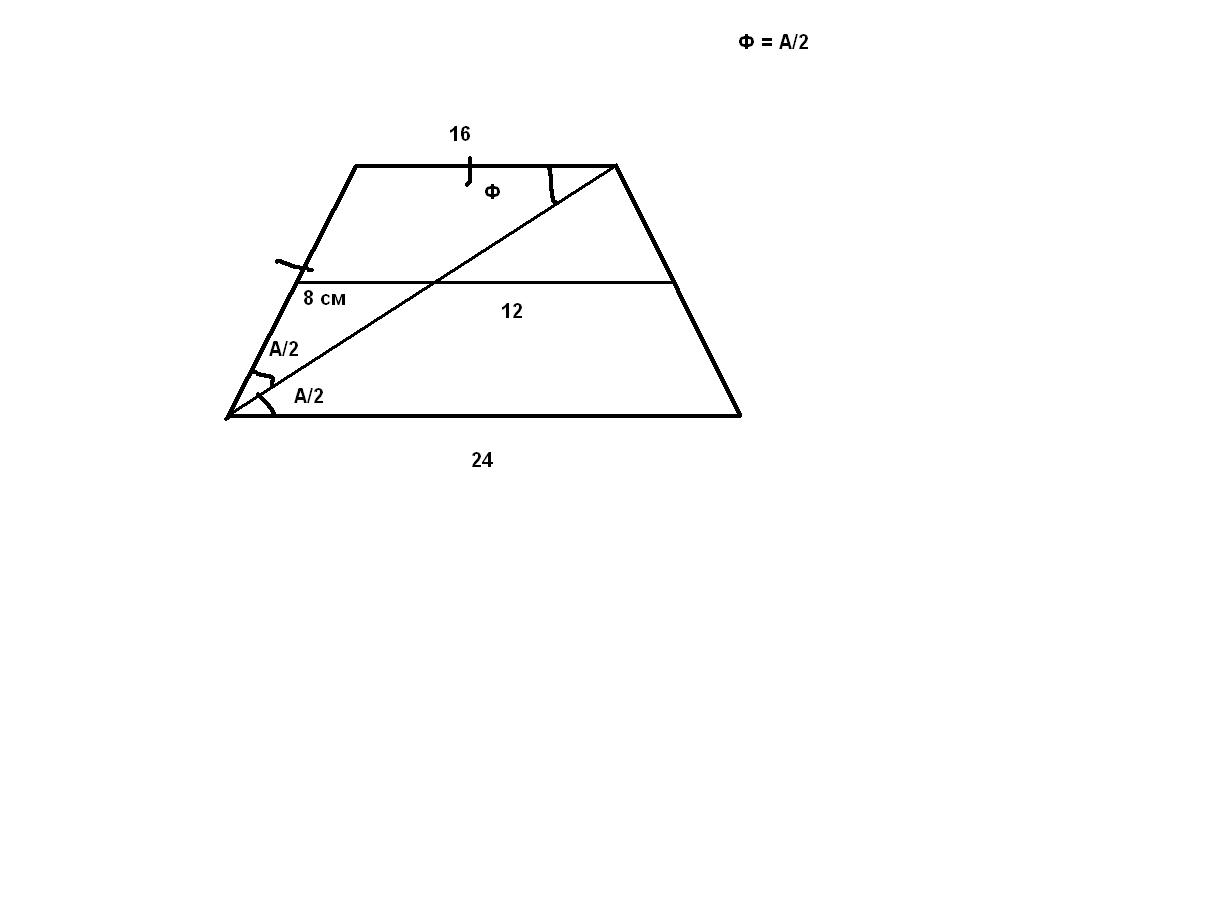
Есть свойство, что биссектриса отсекает от трапеции равнобедренный треугольник, следовательно АВ=ВС=СD. Диагональ делит трапецию на 2 треугольника, средние линии треугольников совпадают со средней линией трапеции. Средняя линия треугольника в 2 раза меньше основания.
Следовательно верхнее основание ВС=8*2=16см
Нижнее основание АD = 12*2=24 cм
Р= 16+16+16+24 = 72 см
