Предмет: Алгебра,
автор: timohfu
Нужен только II-В, Пожалуйста помогите!
Приложения:

Ответы
Автор ответа:
2
Ответ и Объяснение:
Доказательство IIb. Так как a>0 и b>0, то верны неравенства (доказательство: см. рисунок):
Тогда
то есть
что и требовалось.
#SPJ1
Приложения:
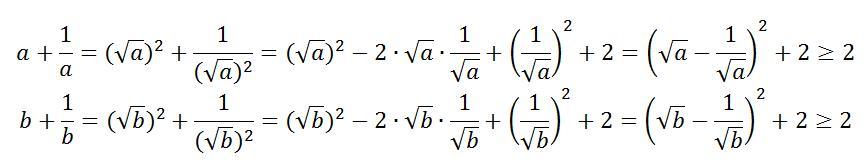
Похожие вопросы