Предмет: Математика,
автор: fuydoyeyiyedy
задние на фото
найти производную функции
Приложения:
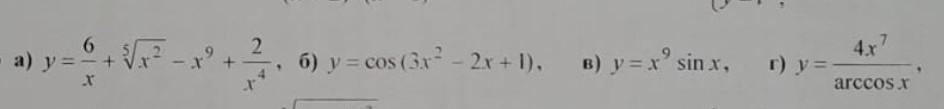
Ответы
Автор ответа:
2
Ответ:
в объяснении
Пошаговое объяснение:
а)
б)
в)
г)
Похожие вопросы
Предмет: Химия,
автор: angryleonarga2009
Предмет: Английский язык,
автор: elizavetaaramnova
Предмет: Українська література,
автор: arinac2022
Предмет: Математика,
автор: nusipkozamahambet
Предмет: Алгебра,
автор: storm1119
https://znanija.com/task/54174611