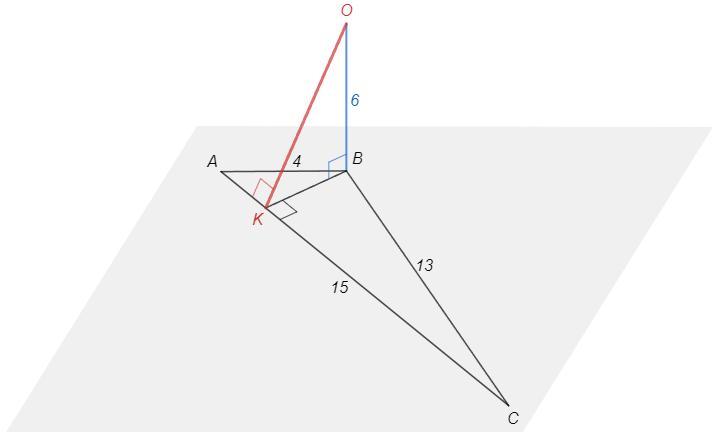
Сторони трикутника дорівнюють 4 см, 13 см, 15 см. 3 вершини більшого кута трикутника до його площини проведено перпендикуляр, довжина якого 6 см. Знайдіть відстань від кінця перпендикуляра до більшої
сторони трикутника.
Ответы
В сантиметрах
AB=4, BC=13, AC=15
В треугольнике против большей стороны лежит больший угол.
AC - большая сторона => ∠ABC - больший угол
По условию из вершины B к плоскости треугольника проведен перпендикуляр OB.
OB⊥(ABC), OB=6
Требуется найти расстояние от точки O до прямой AC.
Расстояние от точки до прямой - длина перпендикуляра.
Проведем перпендикуляр OK к прямой AC.
OK⊥AC
OK - наклонная, B - проекция точки O, BK - проекция наклонной OK
По теореме о трех перпендикулярах если прямая (AC) в плоскости перпендикулярна наклонной (OK), то она перпендикулярна и ее проекции (BK).
OB⊥(ABC), OK⊥AC => BK⊥AC
BK - высота в треугольнике ABC. Найдем её.
Для этого найдем площадь ABC по формуле Герона.
p=(AB+BC+AC)/2 =(4+13+15)/2=16
S=√(p(p-AB)(p-BC)(p-AC)) =√(16*12*3*1)=4*2*3 =24
S=1/2 AC*BK => 24=1/2 15*BK => BK=48/15 =16/5
Если прямая (OB) перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости.
OB⊥(ABC) => OB⊥BK
△OBK - прямоугольный. Найдем OK по теореме Пифагора.
OK =√(OB^2+BK^2) =√(36*25+256)/5 =34/5 (см)