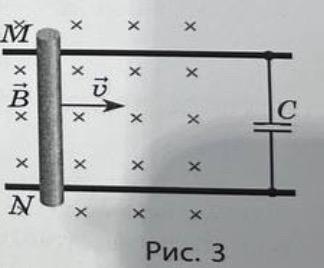
На рис. 3 зображено конструкцію, що
складається з товстих провідних паралельних
рейок
(відстань між рейками 0,2 м), які зʼєднані провідною перемичкою MN і конденсатором С. Уся конструкція
розташована в постійному магнітному полі індукцією 0,8 Тл.
1. Обчисліть значення ЕРС індукції, яка виникає в перемичці, що рухається зі швидкістю 0,1 м/с.
a) 16 мВ;
б) 25 мВ;
B) 100 mB;
г) 400 мВ.
2. З якою швидкістю має рухатися перемичка, щоб на її кінцях виникла різниця потенціалів 0,24 В?
3. Обчисліть заряд, який накопичується на конденсаторі, якщо перемичка рухається зі швидкістю 0,1 м/с. ємність конденсатора 1000 мкФ.
Ответы
1. Згідно з законом електромагнітної індукції, ЕРС індукції, що виникає в перемичці, дорівнює добутку індукції магнітного поля, швидкості переміщення та довжини перемички:
ЕРС = B * v * l
Де:
B - індукція магнітного поля (0,8 Тл)
v - швидкість переміщення (0,1 м/с)
l - довжина перемички (відстань між рейками, 0,2 м)
Підставляючи відповідні значення, отримуємо:
ЕРС = 0,8 * 0,1 * 0,2 = 0,016 В = 16 мВ
Відповідь: а) 16 мВ
2. Задача про різницю потенціалів на кінцях перемички може бути розв'язана з використанням рівняння для роботи сили Лоренца:
W = q * (V2 - V1)
Де:
W - робота сили Лоренца (дорівнює різниці потенціалів на кінцях перемички, 0,24 В)
q - заряд, що накопичується на конденсаторі
V2 - потенціал на одному кінці перемички
V1 - потенціал на іншому кінці перемички
Оскільки перемичка провідна, то потенціали на її кінцях відповідають потенціалам рейок, які дорівнюють 0 В. Тому різниця потенціалів V2 - V1 дорівнює 0,24 В.
Підставляючи відповідні значення, отримуємо:
0,24 = q * 0,24
q = 1 Кл
Отже, заряд, який накопичується на конденсаторі, дорівнює 1 Кл.
Відповідь: 1 Кл
3. Задача про заряд на конденсаторі може бути розв'язана з використанням формули для заряду на конденсаторі:
Q = C * V
Де:
Q - заряд на конденсаторі
C - ємність конденсатора (1000 мкФ = 0,001 Ф)
V - напруга на конденсаторі (дорівнює різниці потенціалів на кінцях перемички, 0,24 В)
Підставляючи відповідні значення, отримуємо:
Q = 0,001 * 0,24 = 0,00024 Кл = 240 мКл
Отже, заряд, який накопичується на конденсаторі, дорівнює 240 мКл.
Відповідь: 240 мКл