Question

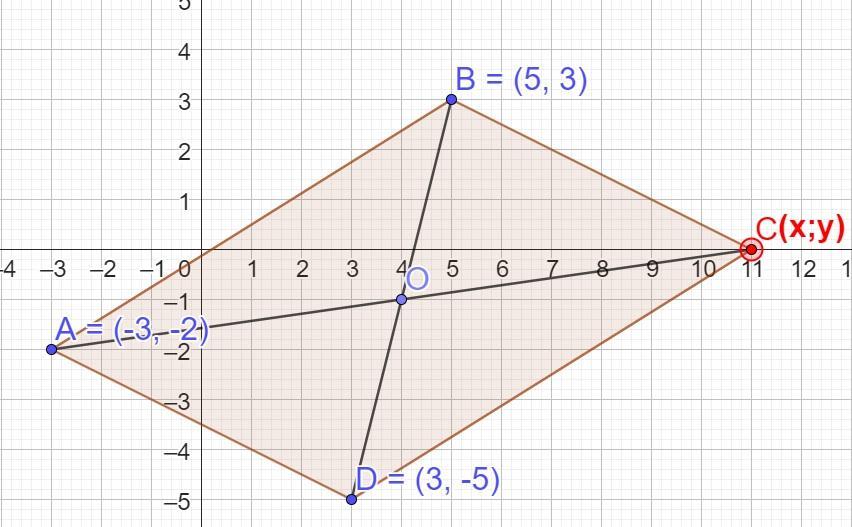
Знайди координати вершини C паралелограма АВСD, якщо А(–3; –2), В(5; 3), D(3; –5). У відповідь запиши суму x+y

Answer 1

Ответ:

Сума координат вершини С паралелограма АВСD: x+y=11

Объяснение:

Знайди координати вершини C паралелограма АВСD, якщо А(–3; –2), В(5; 3), D(3; –5). У відповідь запиши суму x+y.

Для відшукання вершини С  скористаємося властивістю про те, що у паралелограма ABCD діагоналі AC і BD в точці перетину (О) діляться навпіл:

AО=ОC, BО=ОD.

Спочатку знайдемо координати центра О - середини відрізка (діагоналі) ВD за відомими координатами:

$\bf x_O=\dfrac{x_B+x_D}{2} ; \;\;\;\;\;\;y_O=\dfrac{y_B+y_D}{2};$

$x_O=\dfrac{5+3}{2}=\dfrac{8}{4}=\bf 4;$

$y_O=\dfrac{3+(-5)}{2}=\dfrac{-2}{2} =\bf -1$

Отримали O(4; -1) - координати точки перетину діагоналей AC і BD.

Із умови, що AO=OC складаємо рівняння для знаходження координати точки C і розв'язуємо:

$\bf x_O=\dfrac{x_A+x_C}{2} ; \;\;\;\;\;y_O=\dfrac{y_A+y_C}{2};$

$\dfrac{-3+x_C}{2}=4; \;\;\;\;\;\; \dfrac{-2+y_C}{2}=-1;\\\\-3+x_C=8; \;\;\;\;\;\;-2+y_C=-2;\\\\\bf x_C=11; \;\;\;\;\;\;\;\;\;\;\;\;\;\;y_C=0;$

С(11; 0 ) - шукана вершина.

Отже x + y = 11 + 0 = 11

#SPJ1