Яку фігуру утворюють усі точки площини розміщені на однаковій відстані від трьох даних точок що не лежать на одній прямій? А)пряму розміщено на даній відстані від точок
Б)центр кола що проходить через дані точки В) коло з центром в одній з цих точок Г)рівносторонній трикутник з вершинами в цих точках
Ответы
Ответ:
Б) центр окружности проходящий через данные точки
Объяснение:
Перевод: Какую фигуру образуют все точки плоскости, расположенные на одинаковом расстоянии от трех данных точек, не лежащих на одной прямой?
А) прямая размещена на данном расстоянии от точек;
Б) центр окружности проходящий через данные точки;
В) окружность с центром в одной из этих точек;
Г) равносторонний треугольник с вершинами в этих точках.
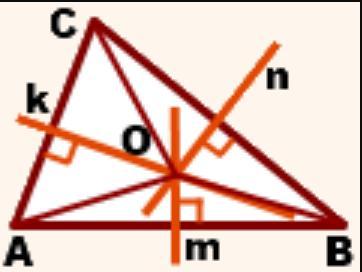
Решение. Пусть точки A, B, C не лежат на одной прямой. Тогда можно построить треугольник ABC.
Делим отрезок AB пополам. Через середину отрезка AB проведём перпендикуляр m к прямой AB. Каждая точка этого перпендикуляра будет равноудалена от точек A и B. Значит, m - серединный перпендикуляр стороны AB треугольника ABC.
Теперь делим отрезок BC пополам. Через середину отрезка BC проведём перпендикуляр n к прямой BC. Каждая точка перпендикуляра n будет равноудалена от точек B и C. Тогда, n - серединный перпендикуляр стороны BС треугольника ABC.
Далее, делим отрезок AC пополам. Через середину отрезка AC проведём перпендикуляр k к прямой AC. Каждая точка этого перпендикуляра будет равноудалена от точек A и C. Отсюда, k - серединный перпендикуляр стороны AC треугольника ABC.
Получается, прямые m, n и k - серединные перпендикуляры треугольника ABC!
Известно свойство серединных перпендикуляров к сторонам треугольника:
- Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Обозначим точку пересечения серединных перпендикуляров буквой О. Так как точка О лежит на перпендикулярах к прямой АВ, BC и AС, то ОA=ОB=ОС. Значит, точка О находится на одинаковом расстоянии от точек А, В и С.
- Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной около этого треугольника окружности.
Значит, точка О – центр окружности описанной около треугольника ABC, то есть окружность пройдёт через все три точки А, В и С.
Этим показали:
Все точки плоскости, расположенные на одинаковом расстоянии от трех данных точек, не лежащих на одной прямой образуют всего лишь центр окружности проходящий через данные точки.
#SPJ1