Question

Отрезок, соединяющий вершину треугольника с его противоположной стороной, делит треугольник на два, каждый из которых подобен исходному треугольнику. Верно ли утверждение, что этот отрезок обязательно перпендикулярен стороне, к которой он проведен?

Answer 1

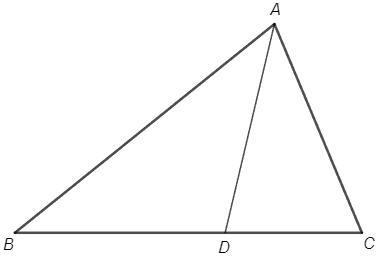
По условию △ADB подобен △ADC при некотором соответствии вершин. Тогда ∠ADB равен некоторому внутреннему углу треугольника ADC.

∠ADB - внешний угол △ADC. Помним, что внешний угол треугольника равен сумме внутренних углов, не смежных с ним. Т.е. внешний угол не может быть равен внутреннему углу не смежному с ним.

Вывод: ∠ADB может быть равен только ∠ADC, а если смежные углы равны, то они оба прямые и AD⊥BC.