Предмет: Алгебра,
автор: sereakolobok5
Как это упростить, зная что, а - просто произвольное число, х намного больше a ?
Приложения:
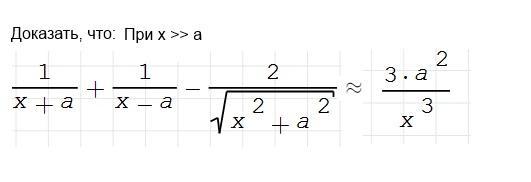
Ответы
Автор ответа:
1
первые две функции разложить в ряд Тейлора до квадратов
Для третьей функции хватит и линейного разложения
Сложим все три выражения, не забыв умножить последнее на -2
много чего уйдет и останется
Автор ответа:
1
Відповідь:
при х >> a
Пояснення:
Приложения:

Похожие вопросы
Предмет: Литература,
автор: goreckaavaleria338
Предмет: Биология,
автор: fupria
Предмет: Информатика,
автор: 7zbgnyj7hn
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: anivardanian09