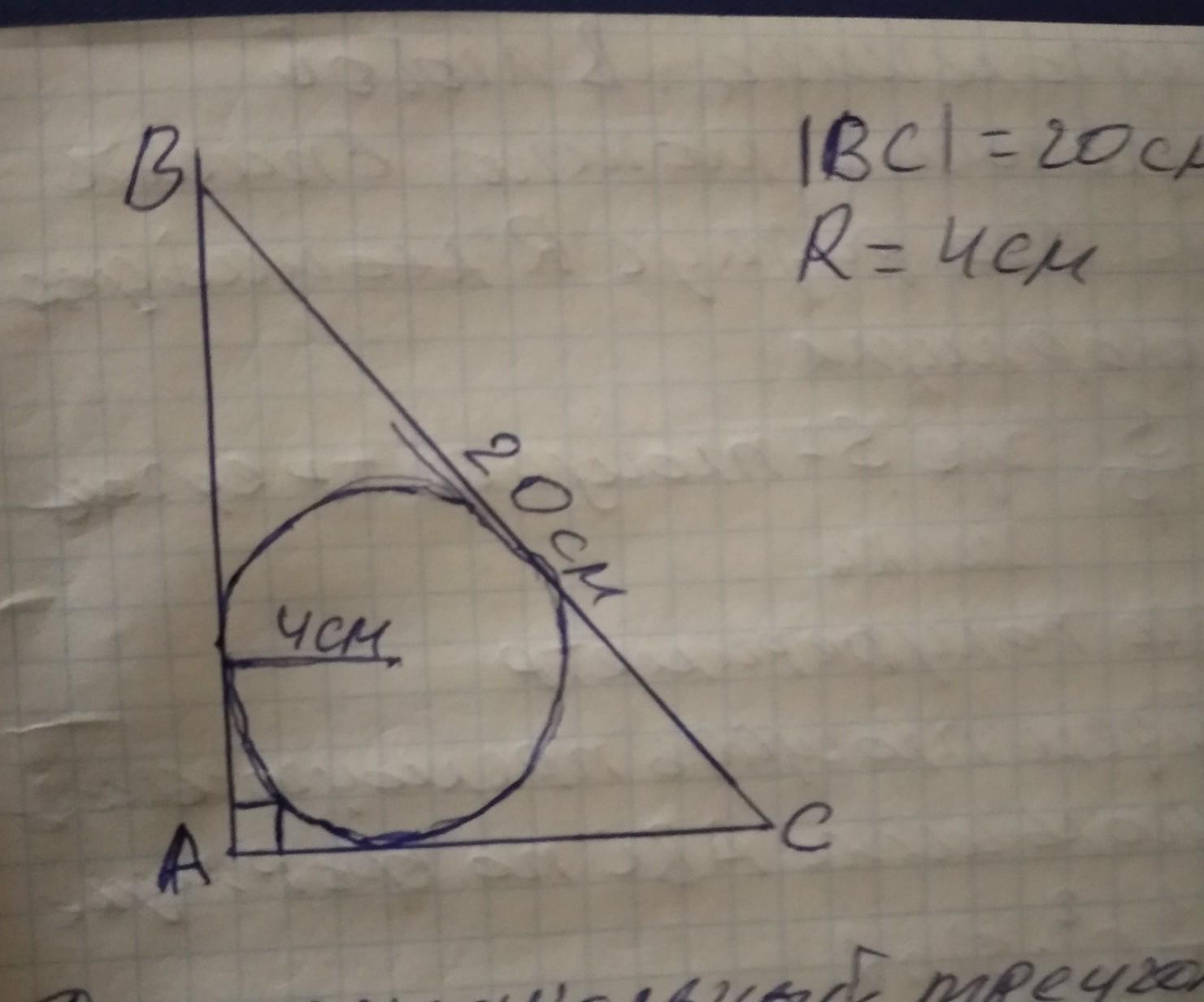
Найдите периметр прямоугольного треугольника, если его гипотенуза равна 20 см, а радиус вписанной окружности 4 см.
Пожалуйста с рисунком, и полным объяснением
Ответы
Ответ:
Периметр прямоугольного треугольника ABC равен 50 сантиметров
Пошаговое объяснение:
Дан прямоугольный треугольник (смотри фотографию). Назовем его ABC. По условию задачи гипотенуза прямоугольного треугольника (сторона BC) равна 20см, а радиус вписанной окружности равен 4см. Нам нужно найти периметр прямоугольного треугольника ABC. Периметром прямоугольного треугольника мы назовем сумму длин его сторон, тоесть сумму длин его катетов и гипотенузы. Полупериметр прямоугольного треугольника мы найдем по формуле:
где a и b катеты прямоугольного треугольника ABC
c-гипотенуза прямоугольного треугольника ABC
Периметр прямоугольного треугольника равен двум его полупериметрам, тоесть
P=2p
Найдем площадь прямоугольного треугольника ABC по формуле: (1)
где угол alpha равен 90° а это прямой угол ABC. Найдем синус прямого угла alpha:
Подставим значения синуса прямого угла alpha и значения длины гипотенузы прямоугольного треугольника в формулу (1) Имеем:
где с-гипотенуза прямоугольного треугольника
угол alpha равен 90° а это угол ABC
Мы нашли площадь прямоугольного треугольника ABC и она равна 100см^2
Найдем периметр прямоугольного треугольника ABC. Нам известно, что в любой прямоугольный треугольник можно вписать окружность, радиус которой найдем по формуле. (2)
где s-площадь прямоугольного треугольника ABC и она равна 100см^2
p-полупертметр прямоугольного треугольника ABC
r-радиус вписанной окружности в прямоугольный треугольник ABC и он равен 4см. Отсюда полупериметр прямоугольного треугольника ABC равен: (3)
Подставим значения площади (s=100см^2) прямоугольного треугольника ABC и радиуса вписанной окружности (r=4см) в формулу (3). Имеем:
Мы нашли полупериметр прямоугольного треугольника ABC и он равен 25см.
Нам известно, что периметр равен двум полупериметрам
Поэтому периметр прямоугольного треугольника равен:
Мы нашли периметр прямоугольного треугольника ABC и он равен 50см
Ответ: Периметр прямоугольного треугольника ABC равен 50 сантиметров.