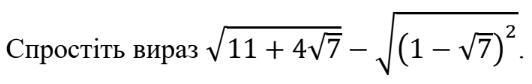
Ответы
Рассмотрим сначала первое слагаемое. Хочется избавится от корня, но избавиться мы можем только, если выделим полный квадрат. В полном квадрате, да и вообще в формулах сокращённого умножения есть удвоенное произведение, стоит его найти!
Заметим, что второе слагаемое можно переписать как . Теперь мы видим, что у нас есть удвоенное произведение, а значит в роле
будет
, а в роле
будет
. Подставим в формулу сокращённого умножения
Мы получили такое же выражение, как под корнем, а значит мы смогли выделить полный квадрат
Ответ:
3.
Объяснение:
√(11 + 4√7) - √(1 - √7)² =
выделим квадрат суммы под знаком первого корня
= √(2² + 2•2•√7 + (√7)²) - √(1 - √7)² =
= √(2 + √7)² - √(1 - √7)² =
воспользуемся тождеством √(х²) = lxl
= l 2 + √7 l - l 1 - √7 l =
выражение, записанное в первом модуле, положительно, т.к. дана сумма двух положительных чисел, а 1 - √7 < 0, т.к. √1 < √7, поэтому
= 2 + √7 - ( - 1 +√7) = 2 + √7 + 1 - √7 = 3.