Предмет: Алгебра,
автор: Dragon444
(1/√x-1/2) (x4 − 4x2 − 5) = 0
Приложения:
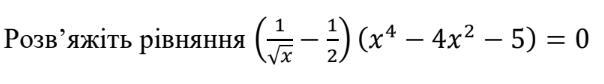
AramHar:
Легенда уже отвечает
Ответы
Автор ответа:
2
Второй множитель я разложил на множители используя следствие из теоремы Виета: если , о первый корень равен
, а второй равен
Потом мы получили произведение из трёх множителей, второй не имел нулей, так как он всегда положительный при всех
После чего мы получили произведение, которое равно нулю, а произведение равно нулю тогда, когда один из множителей равен нулю, а второй не теряет смысла
Но не стоит забывать, что у нас есть в знаменателе корень, а значит подкоренное выражение строго больше нуля, так как знаменатель не может быть нулём, отсюда и строгое неравенство
Похожие вопросы
Предмет: Психология,
автор: pupil902
Предмет: Алгебра,
автор: aimee1xxw
Предмет: Химия,
автор: hakuly
Предмет: Астрономия,
автор: DigestYou
Предмет: Английский язык,
автор: enabockin