Предмет: Алгебра,
автор: sw3toff
Даю 100 баллов Розв’язати диференціальне рівняння, що допускають пониження порядку
Приложения:
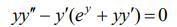
Ответы
Автор ответа:
0
Сделаем замену , тогда
Поделим всё на и
, но не забываем про решение
!
Сделаем ещё одну замену , тогда
Решаем первое уравнение . Теперь решаем второе уравнение
Осталось решить получившееся уравнение
Похожие вопросы
Предмет: Английский язык,
автор: khristya79
Предмет: Українська мова,
автор: angelinass1515
Предмет: Українська мова,
автор: fashiongame111
Предмет: Математика,
автор: Tusiksk