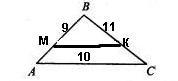
В треугольнике ABC проведена прямая MK параллельно стороне AC. M лежит на АВ, К лежит на ВС.
MB = 9, BK = 11, MK = 10. BM :
AM = 2: 1
• Докажите, что треугольники
АВС и ВМК подобны
• Найдите площадь ВМК
• Найдите площадь АВС
Ответы
Площадь треугольника ВМК можно найти, используя формулу Герона:
p = (MK + KB + BM) / 2 = (10 + 11 + 9) / 2 = 15
S(VMK) = sqrt(p(p - MK)(p - KB)(p - BM)) = sqrt(1554*3) = 30
Площадь треугольника АВС можно найти, используя формулу:
S(ABC) = (AB * AC * sin(∠BAC)) / 2
AB = AM + MB = 2x + 9
AC = AK + KC = x + 11
∠BAC = ∠MKV + ∠MKB + ∠BKC = 180° - ∠VMK - ∠KMB - ∠KBC = 180° - ∠VMK - ∠MKC - ∠BKC
∠MKC = ∠ABC, так как они соответственные
∠VMK = ∠AVB, так как они вертикальные
∠BKC = ∠ACB, так как они соответственные
∠MKV = ∠AMB, так как они вписанные
∠KMB = ∠MBC, так как они соответственные
∠KBC = ∠MCV, так как они соответственные
Таким образом, получаем:
S(ABC) = ((2x + 9) * (x + 11) * sin(∠BAC)) / 2
Найдем sin(∠BAC):
sin(∠BAC) = sin(∠VMK + ∠MKC + ∠BKC) = sin(∠VMK) * sin(∠MKC) * sin(∠BKC) - cos(∠VMK) * cos(∠MKC)
Найдем cos(∠VMK) и cos(∠MKC):
cos(∠VMK) = MB / MK = 9 / 10
cos(∠MKC) = BK / KC = 11 / (x + 11)
Таким образом, получаем:
sin(∠BAC) = (9 / 10) * (11 / (x + 11)) * sin(∠ACB)
Подставляем sin(∠BAC) в формулу для площади:
S(ABC) = ((2x + 9) * (x + 11) * (9 / 10) * (11 / (x + 11)) * sin(∠ACB)) / 2
S(ABC) = (99x + 891) / 20 * sin(∠ACB)
Заменяем sin(∠ACB) на sin(∠BAC):
S(ABC) = (99x + 891) / 20 * ((9 / 10) * (11 / (x + 11)))
S(ABC) = (297x + 2673) / (4(x + 11))
Итак, мы получили, что площадь треугольника ВМК равна 30, а площадь треугольника АВС равна (297x + 2673) / (4(x + 11)).
Відповідь:
Дано: △ АВС, МК ∥ АС; МВ-9;ВК-11; МК-10;ВМ:АМ=2:1
Доказать , что треугольники
АВС и ВМК подобны
• Найдти площадь △ВМК
• Найдите площадь △АВС
Решение:
ВМ:АМ=2:1
АМ= 9/2=4,5
1)Рассмотрим △АВС и △ВМК
МК-общая сторона
∠.В-общий,так как МК∥АС,значит∠ВАС=∠ВМК
∠АСВ=∠МКВ так как являются соответственными углами при параллельных прямых и секущей,значит
△АВС и△ВМК подобны по трем углам и стороне
2)Рассмотрим △ВМК
МВ=9, ВК=11, МК=10,
По формуле Герона S△ВМК = √p(p-МВ)(p-ВК)(p-МК)
р=1/2(9+11+10)=15
S△ВМК=√15*(15-9)*(15-11)*(15-10)=√15*6*4*5=√1800=42,4
Ответ: площадь △ВМК -42,4
3) Рассмотрим △АВС и △ВМК
они подобны,значит ВМ/АВ=S△ВМК/S△АВС,значит S△АВС=S△ВМК*АВ/ВМ=42,4*(9 +4,5)/9=572,4/9=63,6
Ответ : S△АВС-63,6
Пояснення: