Предмет: Алгебра,
автор: Ffhh54
Найдите производную функции
Приложения:
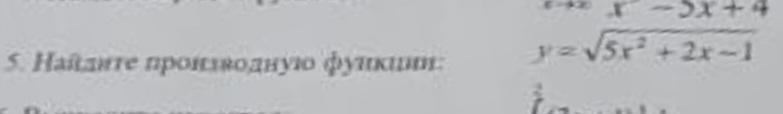
Ffhh54:
y= которое
Ответы
Автор ответа:
1
Формулы, который нам понадобятся для поиска производной:
Функция сложная, значит нам нужно сначала найти производную от корня, а потом производную от подкоренного выражения:
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: vbocokin
Предмет: Физика,
автор: gm8331877
Предмет: Физика,
автор: rimmabulgakova86
Предмет: Алгебра,
автор: dianamusaitova
Предмет: Английский язык,
автор: galiadmitrisina20190