Предмет: Математика,
автор: g02526750
Знайдіть інтеграли, використовуючи метод інтегрування частинами
Приложения:
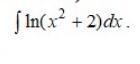
Ответы
Автор ответа:
1
Ответ:
Метод интегрирования по частям : .
Приложения:

Похожие вопросы
Предмет: Химия,
автор: nastya070104
Предмет: Математика,
автор: kirakarnaykhova12
Предмет: Математика,
автор: Aaa77558
Предмет: Английский язык,
автор: monikatortaeva03
Предмет: Биология,
автор: ibrohimjonahmadjonov