Question

Терміново!!! Дам 100!

Answer 1

Задача:

Доведіть рівність двох трикутників за медіаною та кутами, на які ця медіана ділить кут трикутника.

Дано:

ΔАВС і ΔА₁В₁С₁,

АМ=А₁М₁ - медіани

∠ВАМ=∠В₁А₁М₁,  ∠МАС=∠М₁А₁С₁

Довести: ΔАВС=ΔА₁В₁С₁

Доведення:

Нехай у ΔАВС і ΔА₁В₁С₁ рівні медіани АМ=А₁М₁, а також ∠ВАМ=∠В₁А₁М₁  і  ∠МАС=∠М₁А₁С₁;

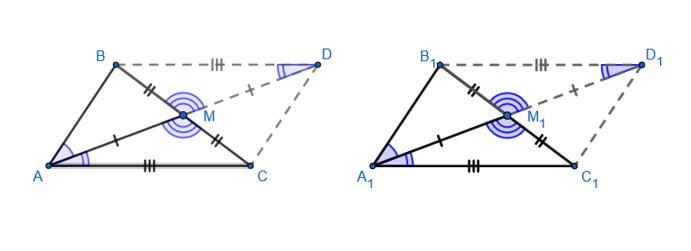
На прямій АМ у напівплощині протилежній тій, в якій лежить відрізок АМ, відносно прямої ВС відкладемо відрізок МD, рівний відрізку АМ;

∠ВМD=∠АМС - як вертикальні;

АМ - медіана ΔАВС ⇒ ВМ = МС;

ΔАМС=ΔВМD за першою ознакою, тому BD = AC та ∠MDB=∠MAC;

Аналогічні побудови проведемо для ΔА₁В₁С₁, тоді:

ΔА₁М₁С₁=ΔВ₁М₁D₁, звідси В₁D₁=А₁С₁ та ∠М₁D₁B₁=∠М₁А₁С₁;

Так як АМ=А₁M₁, то АD=2АМ=2А₁M₁=А₁D₁;

∠МDB=∠МАС=∠М₁А₁С₁=∠М₁D₁B₁;

Таким чином, ΔАВD=ΔА₁В₁D₁ за другою ознакою, що означає АВ=А₁В₁ і B₁D₁=BD  ⇒  АС=А₁C₁;

∠ABC=∠BАM+∠МАС=∠B₁А₁M₁+∠М₁А₁С₁=∠A₁B₁C₁;

Отже, ΔАВС=ΔA₁B₁C за першою ознакою, що й потрібно було довести.