Предмет: Алгебра,
автор: Viscount
Вычислить cos a, если sin a=0,3 и
-7π/2 < а < -5π/2
Приложения:
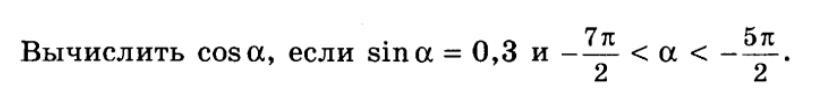
Ответы
Автор ответа:
1
Ответ:
.
Объяснение:
Для вычисления cos a, если sin a=0,3 и -7π/2 < а < -5π/2, мы можем использовать тригонометрический тождественный метод.
Сначала мы можем использовать тождество sin^2 a + cos^2 a = 1, чтобы найти cos a. Заменим sin a на 0,3 и решим уравнение:
sin^2 a + cos^2 a = 1
0,3^2 + cos^2 a = 1
cos^2 a = 1 - 0,09
cos^2 a = 0,91
Затем мы можем взять квадратный корень из обеих сторон, чтобы найти cos a:
cos a = ±√0,91
Так как угол a лежит в третьем и четвертом квадрантах, где cos a < 0, мы можем выбрать отрицательный знак:
cos a = -√0,91 ≈ -0,9539[1].
Таким образом, cos a примерно равен -0,9539.
Похожие вопросы
Предмет: Химия,
автор: vealils8
Предмет: Литература,
автор: zeynabmay41
Предмет: Английский язык,
автор: uaa58418
Предмет: Физика,
автор: emir2205