Question

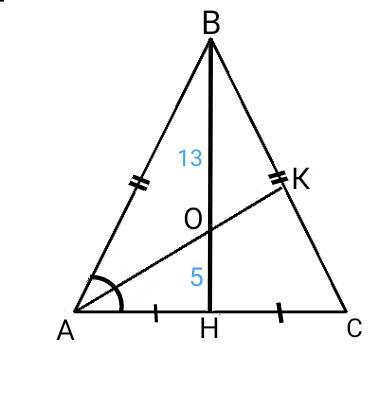
Бісектриса кута при основi рiвнобедреного трикут- ника дiлить його висоту, проведену до основи, на відрізки довжиною 5 см і 13 см, рахуючи від ос- нови трикутника. Знайдіть площу цього трикутника. даю 25 балов ​сроно пожалуйста

Answer 1

Ответ:

135 см².

Объяснение:

1. Пусть ∆ АВС - данный равнобедренный треугольник, АК - биссектриса, ВН - высота, проведённая к основанию.

В ∆ АВН отрезок АО - биссектриса По теореме АО делит сторону треугольника АН на отрезки, пропорциональные сторонам АВ и АН, тогда

АН / АВ

= НО / ОВ =

5 / 13,

ВН = НО + ОВ = 5 + 13 = 18 (см).

2. Пусть х см в одной части, тогда АН = 5х см, АВ = 13х см.

В ∆ АВН по теореме Пифагора

АВ² = АН² + ВН²

(13х)² = 18² + (5х)²

169х² = 324 + 25х²

144х² = 324

х² = 2,25

х > 0, х = 1,5.

Получили, что

АН = 5•1,5 = 7,5 (см).

Так как высота ВН, проведённая к основанию равнобедренного треугольника, является медианой, то АС = 2 • АН = 7,5 • 2 = 15 (см).

3.

S ∆ ABC = 1/2 • AC • BH

= 1/2 • 15 • 18 =

135 (см²).