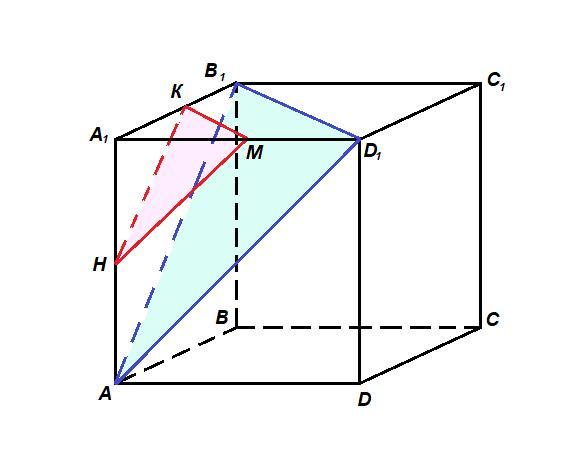
Дано: ABCDA1B1C1D1куб, K середина A1B1, AA1=8
Пострить сесение через K||(AB1D1)
Найти Sсеч

Ответы
Ответ:
Sсеч. = 8√3
Объяснение:
Признак параллельности плоскостей:
- если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
В плоскости (A₁B₁C₁) проведем КМ║B₁D₁.
Так как К - середина А₁В₁ и КМ║B₁D₁, то М - середина A₁D₁ по теореме Фалеса.
В плоскости (АА₁D₁) проведем МН║AD₁.
Так как М - середина A₁D₁ и МН║AD₁, то Н - середина АА₁ по теореме Фалеса.
Соединим точки К и Н.
Итак, КМ║B₁D₁, МН║AD₁, значит (КМН)║(AB₁D₁) по признаку параллельности плоскостей.
КМН - искомое сечение.
ΔАВ₁D₁ равносторонний, так как его стороны - диагонали равных квадратов.
АВ₁ = АА₁√2 = 8√2 как диагональ квадрата.
По формуле площади правильного треугольника:
КМ = 0,5 B₁D₁ как средняя линия ΔA₁B₁D₁.
МН = 0,5 AD₁ как средняя линия ΔAA₁D₁.
НК = 0,5 АВ₁ как средняя линия ΔАА₁В₁.
Значит, ΔКМН ~ ΔAB₁D₁ по трем пропорциональным сторонам с коэффициентом 0,5.
- Площади подобных треугольников относятся как квадрат коэффициента подобия.