Question

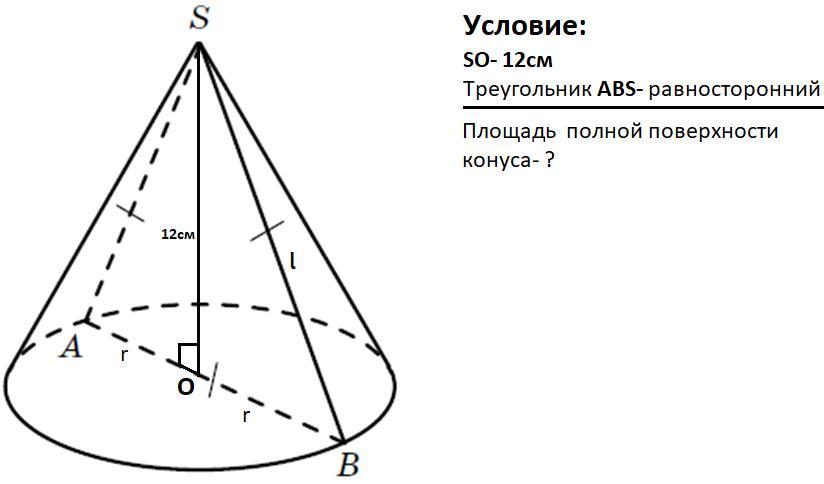
(200 Балів) Знайти площу повної поверхні конуса, якщо його висота дорівнює 12 см, а осьовий переріз конуса – правильний трикутник.

Answer 1

Ответ:

S= 144π

Объяснение:

!Рисунок к задаче закреплен с низу

Разберем задачу поэтапно и решим ее:

1. Для начало разберём самое главное, формулу полной площади конуса:

S= Sосн + Sбок

Sосн= πr²

Sбок= πrl

l- образующая

↓

S=πr²+πrl

2. Разобрав формулу будем постепенно находить неизвестные части:

1) Рассмотрим ΔABS, он равносторонний → все углы равны ∠60°.

2) Теперь рассмотрим ΔВSO- он прямоугольный, а ∠OBS равен 60° → ∠OSB равен 30° →  2OB=BS (но почему так?):

Правило: в прямоугольном треугольнике катет что лежит на против угла 30° в два раза меньше гипотенузы.

Теперь выразив ОВ=x → BS=2х мы можем составить уравнения по теореме Пифагора( но о чем же эта теорема?)

Теорема Пифагора:   в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

↓

$(2x)^{2} =x^{2} +12^{2} \\\\4x^{2} =x^{2} +144\\\\3x^{2} =144\\\\x^{2} =48\\\\x_{1} =4\sqrt{3} \\x_{2} -4\sqrt{3}$

x2 не подходит так как длина катета не может быть отрицательной.

3. Теперь найдя х=r=4√3см мы можем найти площадь основы конуса:

$S=(4\sqrt{3} )^{2} \pi \\\\S=48\pi$

Вот мы и нашли площадь основы конуса.

4. Теперь осталось найти площадь боковой поверхности конуса. Но как ? Помним что в формуле присутствует "l" - образующая.

l=BS=2OB → l=8√3 см

Теперь осталось подставить значения в формулу и найти площадь боковой поверхности конуса:

$S=4\sqrt{3} *8\sqrt{3} *\pi \\\\S=96\pi$

5. Так как мы нашли все неизвестные части формулы осталось их подставить и найти площадь полной поверхности конуса:

$S=48\pi +96\pi \\\\S=144\pi$