Предмет: Математика,
автор: Zhopatebe1
Буду очень благодарна за более детальное объяснение. Не совсем поняла как решать.
Приложения:
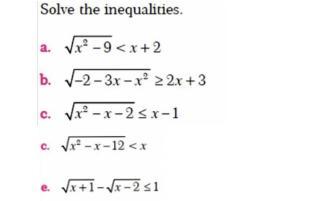
Zhopatebe1:
Спасибо что отвечаете на мой вопрос>:))
Ответы
Автор ответа:
0
Ответ:
Возьмем пример 1 Область допустимых значений x = (- ∞ , 3] ∪ [3 , +∞)
Теперь, найдем допустимые значения для x+2 он у нас может принимать несколько значений
x+2 ≥ 0
x+2 < 0
Но так как то второй вариант нам не подходит
В первом случае
А значит: x = [-2 ,+∞)
Найдем точки пересечения двух переменных
x = [-2 ,+∞) и x = (- ∞ , 3] ∪ [3 , +∞)
Тогда наши точки пересечений будут равны x = [3 ,+∞)
P.S Hулями и меньше функция x+2 ≥ 0 быть не может
Ответ: x = [3 ,+∞)
Надеюсь получилось внятно обьяснить, если еще есть вопросы пиши в коментарии)
Похожие вопросы
Предмет: Геометрия,
автор: vikaomelchenko2010
Предмет: Химия,
автор: a6948373
Предмет: Алгебра,
автор: lklkllvvo
Предмет: Русский язык,
автор: gulzatburataeva
Предмет: Химия,
автор: shelldik2006