Question

Вычислить площадь фигуры ограниченной следующими линиями:

y=(x—1)2 , x2—0,5y2=1.

Answer 1

Ответ: S = 2,09

Пошаговое объяснение: x² - 0,5y² = 1 выразим через у:

$x^{2} -0,5y^{2} =1$

$2x^{2} -y^{2} =2$

$2x^{2} -2=y^{2}$

$y=\sqrt{2x^{2} -2}$

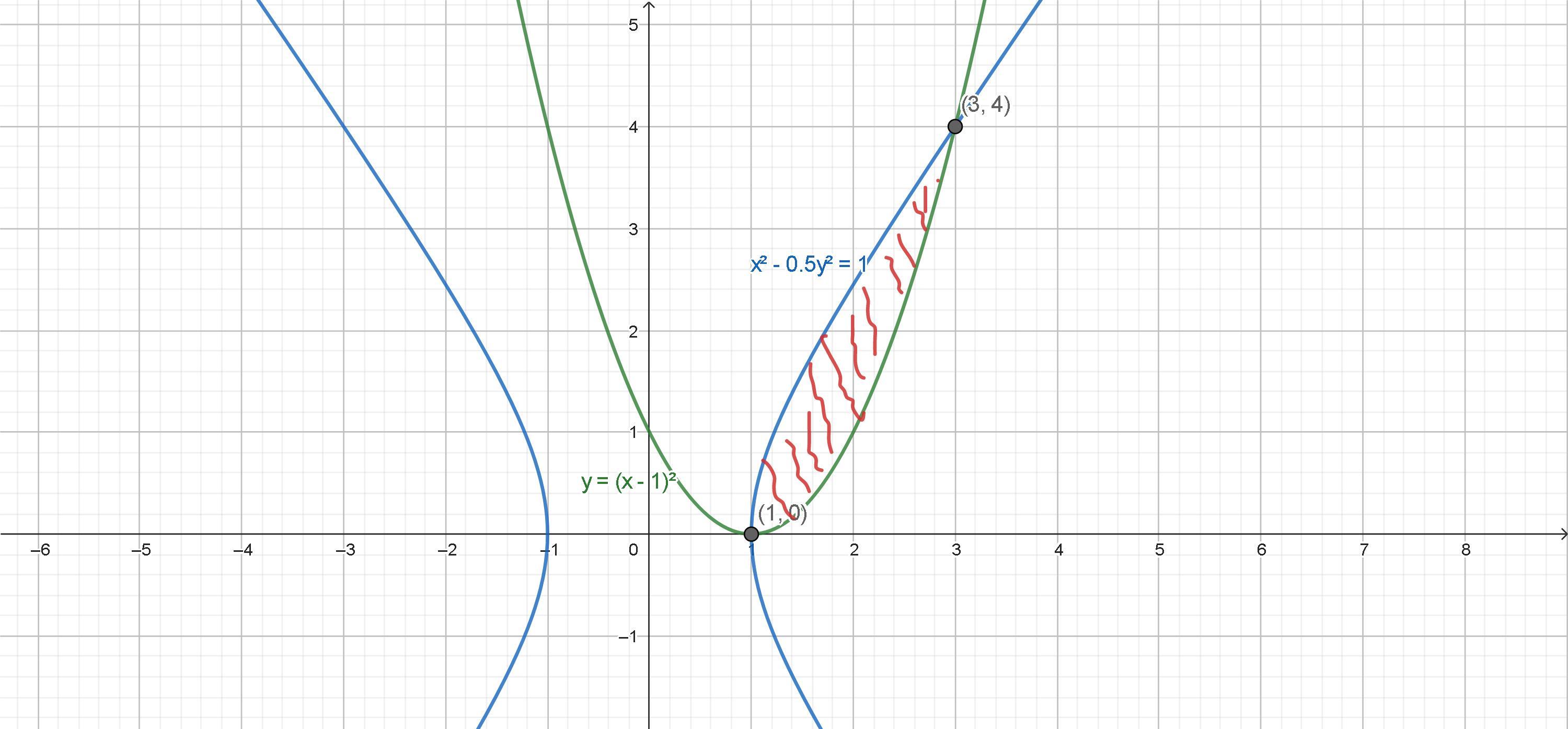
Выявим нашу фигуру на графике. Нарисуем линии данных функции. Площадь фигуры, которую надо найти, отмечена красным.

Как видим, линия функции x² - 0,5y² = 1 лежит выше чем линия функции y = (x - 1)². Поэтому от первого отнимаем вторую и подставим под интеграл:

$\int\limits {(\sqrt{2x^{2} -2} -(x - 1)^{2} )} \, dx$

Теперь нам нужно узнать пределы интеграла. Их можно найти либо через систему двух заданных уравнений либо через график. Воспользуемся вторым.

Посмотрим на график. Область отмеченная красным находится между 1 и 3 на оси Ох. Поэтому определим наш неопределенный интеграл, подставив пределы, и интегрируем:

$S=\int\limits^3_1 {(\sqrt{2x^{2} -2} -(x - 1)^{2} )} \, dx =\int\limits^3_1 {\sqrt{2} *\sqrt{x^{2} -1} } \, dx -\int\limits^3_1 {(x - 1)^{2} } \, dx =$

$=\sqrt{2} \int\limits^3_1 {\sqrt{x^{2} -1} } \, dx -\int\limits^3_1 {(x - 1)^{2} } \, d(x-1) =(*)$

Найдем первый интеграл отдельно:

$\int\limits {\sqrt{x^{2} -1} } \, dx =|\left \{ {{x=sec\theta} \atop {dx=tg\theta*sec\theta d\theta}} \right., sec^{2} \theta-1=tg^{2} \theta |=\int\limits {\sqrt{sec^{2} \theta -1} } \, tg\theta*sec\theta d\theta =$

$=\int\limits {\sqrt{tg^{2} \theta } } \, tg\theta*sec\theta d\theta =\int\limits {tg^{2} \theta *sec\theta \, d\theta =\int\limits {(sec^{2} \theta -1)*sec\theta \, d\theta =$

$=\int\limits {(sec^{3} \theta -sec\theta )\, d\theta =\frac{1}{2} sec\theta tg\theta +\frac{1}{2} ln|sec\theta +tg\theta |-ln|sec\theta +tg\theta |=$

$=\frac{1}{2} sec\theta tg\theta -\frac{1}{2} ln|sec\theta +tg\theta |=\frac{1}{2} x\sqrt{x^{2} -1} -\frac{1}{2} ln|x +\sqrt{x^{2} -1} |$

$(*)=\sqrt{2} (\frac{1}{2} x\sqrt{x^{2} -1} -\frac{1}{2} ln|x +\sqrt{x^{2} -1} |)|^{3}_{1} -\frac{(x-1)^{3} }{3} |^{3}_{1} =(\frac{1}{\sqrt{2} } *3\sqrt{3^{2} -1} -\frac{1}{\sqrt{2} } ln|3 +$

$+\sqrt{3^{2} -1} |-\frac{1}{\sqrt{2} } \sqrt{1^{2} -1} +\frac{1}{\sqrt{2} } ln|1 +\sqrt{1^{2} -1} |)-\frac{(3-1)^{3} }{3} +\frac{(1-1)^{3} }{3} =$$=(\frac{1}{\sqrt{2} } *3\sqrt{8} -\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} |-0+\frac{1}{\sqrt{2} } ln|1 +0} |)-\frac{2^{3} }{3} +\frac{0^{3} }{3} =$

$=(\frac{1}{\sqrt{2} } *3*2\sqrt{2} -\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} |+\frac{1}{\sqrt{2} } ln1)-\frac{8}{3} +0=6-\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} |-\frac{8}{3} =$

$=5\frac{3}{3} -2\frac{2}{3} -\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} |=3\frac{1}{3} -\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} |=\frac{10}{3} -\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} |$.

Площадь фигуры равна:

$S=\frac{10}{3} -\frac{1}{\sqrt{2} } ln|3 +\sqrt{8} | = 2,086882$