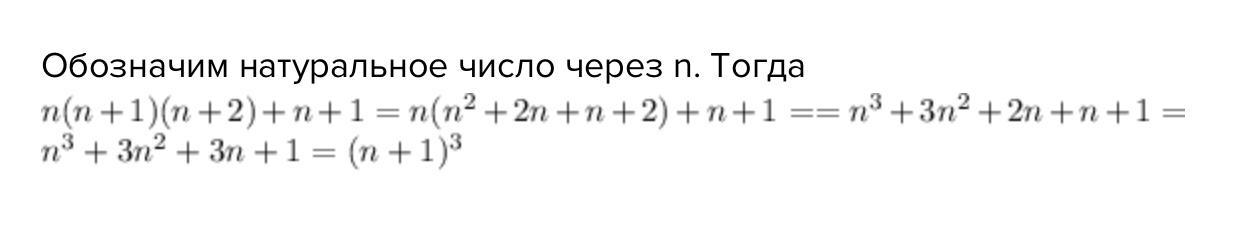Завдання 1-етапу Всеукраїнської учнівської олімпіади з математики 2022-2023 m.p 8 клас
1.Доведіть, що добуток трьох послідовних натуральних чисе, складений з другим із них, є кубом другого числа,
2. Є лист паперу в клітинку і олівці 6 кольорія кафку число клітин так, щоб для будь-яких двох кольорів знайшлося деi aim цих кольорів, що граничать по стороні Доведіть, зафарбувати не можна. то клим х
3. На острові проживають 2010 мешканцію у (завжди говорить правду), або брехун (завжди бреме). Одоор жителі острова розбилися на пари, і кожен пр одну із фраз: «він лицар» або «він брехукм. Чи могло ися так, що тих і інших фрая було виголошено порівну
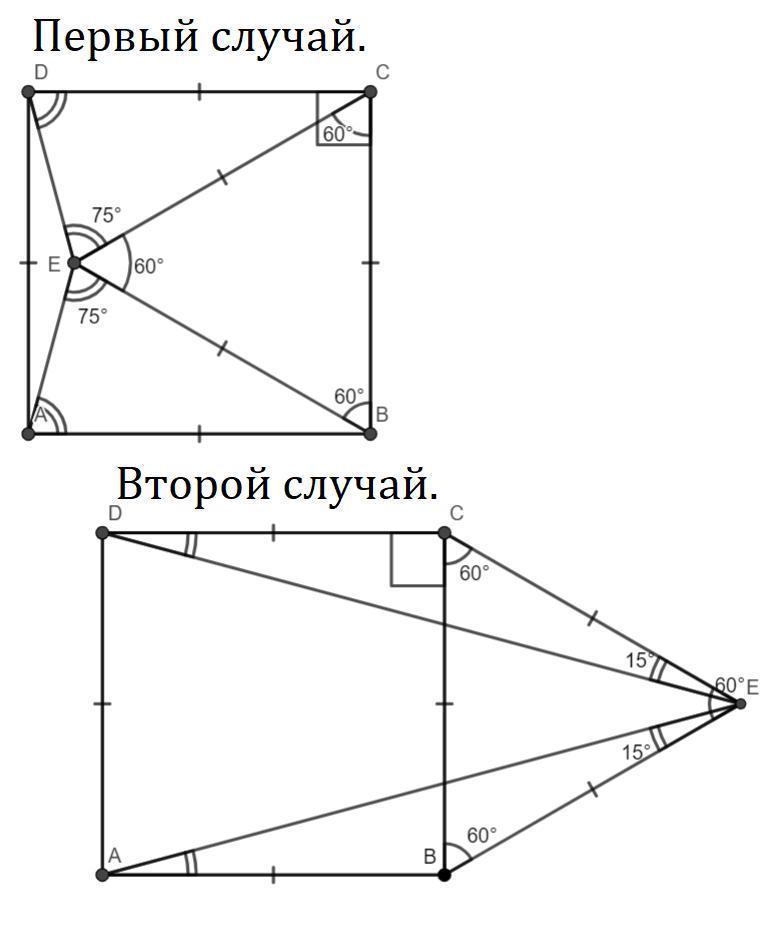
4. ABCD - квадрат, AD=BE=CE. Знайдіть AKD 5. € числа 1, 2, 4, 6 До коляеться вибрати будь-які да я их чеr i помножити їх на одне і те ж натуральне число. Чи мо таких операцій уробити всі числа рівними

Ответы
це ваша відповідь на 1. Запитання (фото)
2.2.Розв’язання. З умови випливає, що існують клітини кожного кольору. Якщо якогось кольору буде тільки одна клітина, то в неї має бути 5 різнокольорових сусідів, що неможливо. Отже, кожного кольору хоча б по дві клітини, а всього - не менше 12 клітин.
3.Нет не может быть не равные количества голосов получиться
4.Все стороны квадрата равны: AB = BC = CD = AD.Сумма внутренних углов треугольника равна 180°.По условию BE = EC, поэтому т. Е лежит на серединном перпендикуляре к BC. Раз BE = AD > BC/2, то точка Е может лежать в двух разных полуплоскостях относительно BC.ΔCEB - правильный, поскольку BE = EC = BC. Поэтому ∠ECB = ∠CBE = ∠BEC = 180°:3 = 60°.∠DCB = ∠CBA = 90°, как углы квадрата ABCD.Первый случай: d(E, AD) < AB (точка Е в левой полуплоскости от BC, по моему рисунку).∠DCE = ∠DCB-∠ECB = 90°-60° = 30°.ΔDCE - равнобедренный (EC = CD), поэтому углы при основании DE равны;∠DEC = ∠EDC = (180°-∠DCE):2 = (180°-30°):2 = 150°:2 = 75°.Аналогично ∠ABE = ∠ABC-∠CBE = 30°,ΔABE - равнобедренный (BA = BE), ∠BAE = ∠BEA = (180°-∠ABE):2 = 75°.∠AED, ∠DEC, ∠CEB и ∠BEA составляют полный угол (360°), поэтому∠AED = 360°-(∠DEC+∠CEB+∠BEA) = 360°-(75°+60°+75°) = 360°-210° = 150°.Второй случай: d(E, AD) > AB (точка Е в правой полуплоскости от BC, по моему рисунку).∠DCE = ∠DCB+∠ECB = 90°+60° = 150°.ΔDCE - равнобедренный (EC = CD), поэтому углы при основании DE равны;∠DEC = ∠EDC = (180°-∠DCE):2 = (180°-150°):2 = 30°:2 = 15°.Аналогично ∠ABE = ∠ABC+∠CBE = 150°,ΔABE - равнобедренный (BA = BE), ∠BAE = ∠BEA = (180°-∠ABE):2 = 15°.∠AED, ∠DEC и ∠BEA составляют ∠CEB = 60°, поэтому∠AED = ∠CEB-(∠DEC+∠BEA) = 60°-(15°+15°) = 60°-30° = 30°.Ответ: 150° или 30°.(фото+)