Question

ДАЮ 55 БАЛЛОВ! НУЖНА ПОМОЩЬ!

Answer 1

Ответ:

Установили соответствие между началом предложения (1 - 4) и его окончанием (А-Д):

1 → Б

2 → В

3 → Г

4 → А

Объяснение:

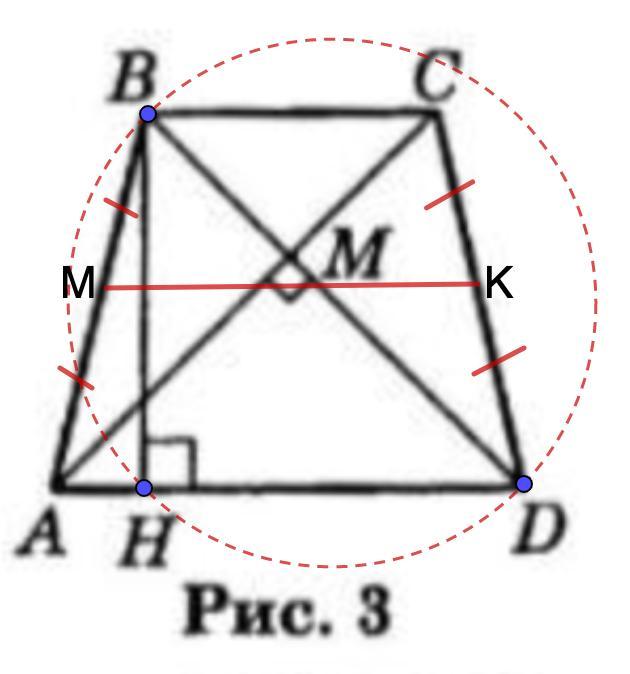
На рисунке с показана равнобедренная трапеция ABCD, диагонали которой перпендикулярны, высота трапеции равна 10.

Установите соответствие между началом предложения (1 - 4) и его окончанием (А-Д) так, чтобы образовалось верное утверждение.

1 Диагональ АС трапеции равна ...

2 Средняя линия трапеции равна ...

3 Площадь трапеции ABCD равна ...

4 Радиус окружности, описанной вокруг треугольника BHD, равен ...

A 5√2

Б 10√2

B 10

Г 100

Д 100√2

Дано: АВСВ - равнобедренная трапеция;

АС ⊥ BD  - диагонали;

ВН = 10 - высота;

МК - средняя линия.

Найти: АС; МК; S(ABCD);  R описанной окружности около ΔBHD.

Решение:

Вспомним свойства равнобедренной трапеции:

• В равнобедренной трапеции со взаимно перпендикулярными диагоналями высота равна средней линии.

⇒ ВН = МК = 10

• Средняя линия трапеции равна полусумме оснований.

⇒   $\displaystyle\bf MK=\frac{BC+AD}{2} =10$

В равнобедренной трапеции высота, опущенная из вершины тупого угла, делит большее основание на части, большая из которых равна полусумме оснований.

⇒   $\displaystyle\bf HD=\frac{BC+AD}{2} =10$

1. Найдем АС.

Рассмотрим ΔHBD - прямоугольный.

По теореме Пифагора найдем BD:

BD² = BH² + HD² = 100 + 100 = 200

BD = √200 = 10√2

• В равнобедренной трапеции диагонали равны.

⇒ BD = AC = 10√2

Ответ: 1 → Б

2. Найдем МК.

МК = ВН = 10

Ответ: 2 → В

3. Найдем S(ABCD).

• Площадь трапеции равна произведению полусуммы оснований на высоту.

$\displaystyle\bf \frac{BC+AD}{2} =10;\;\;\;\;\;BH = 10\\\\S(ABCD) = 10\cdot10 = 100$

Ответ: 3 → Г

4. R описанной окружности около ΔBHD.

ΔBHD - прямоугольный.

• Центр описанной окружности около прямоугольного треугольника лежит в середине гипотенузы.

⇒ BD  - диаметр.

• Радиус равен половине диаметра.

⇒ R = BD : 2 = 10√2 : 2 = 5√2

Ответ: 4 → А