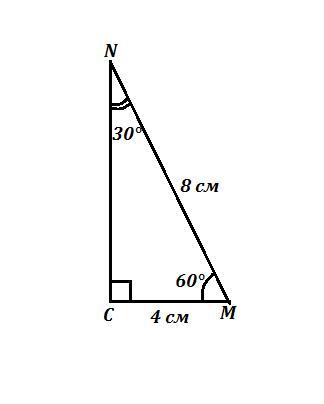
у прямокутному трикутнику CMN з прямим кутом C кут M = 60 градусів, MN = 8 см, Тоді катет CN =?
Ответы
Ответ:
В прямоугольном треугольнике ABC:
∠C =90°
∠B = 60°
∠A = 180 - 90 - 60 = 30 (°)
Катет BC, противолежащий углу 30°, равен половине гипотенузы.
BC = AB / 2
BC = 8/2 = 4 (cм)
По теореме Пифагора:
AB² = BC² + AC²
8² = 4² + AC²
AC² = 64 - 16
AC² = 48
AC = √48
AC = 4√3 (см)
-----------------------------------------------------------------------------------------------
Косинусом угла А является отношение прилежащего к нему катета AC к гипотенузе AB.
cos A = AC / AB
cos 30° = √3 / 2
AC / 8 = √3 / 2
2AC = 8√3
AC = 4√3 (cм)
----------------------------------------------------------------------------------------------
Синусом угла B Является отношение противолежащего ему катета АС к гипотенузе АВ.
sin B = AC / AB
sin 60° = √3 / 2
AC / 8 = √3 / 2
2AC = 8√3
AC = 4√3 (cм)
Решение.
ΔCMN - прямоугольный , ∠С=90° , MN=8 см , ∠М=60° .
Найти СN .
Сумма острых углов прямоугольного треугольника равна 90° , так как 180°-90°=90° .
Значит ∠М+∠N=90° ⇒ ∠N=90°-∠M=90°-60°=30° .
В прямоугольном треугольнике против против угла в 30° лежит катет, равный половине гипотенузы , значит СМ=8:2=4 см .
Тогда по теореме Пифагора MN²=CM²+CN² ⇒ CN²=MN²-CM² ,
CN²=8²-4²=64-16=48 , CN=√48=√(16·3)=4√3 см
Ответ: CN=4√3 см .