Предмет: Математика,
автор: maximchik009
Помогите пожалуйста с решением
Приложения:
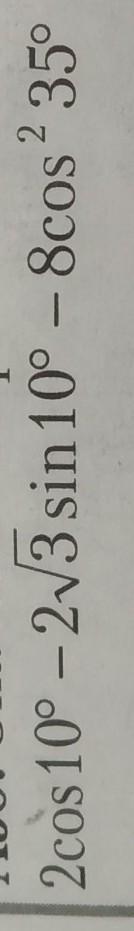
Ответы
Автор ответа:
3
Ответ:
- 4.
Пошаговое объяснение:
Вычислить
Воспользуемся формулами
Тогда получим
Похожие вопросы
Предмет: Русский язык,
автор: starartem
Предмет: Русский язык,
автор: вышивала
Предмет: Русский язык,
автор: bajrak
Предмет: Алгебра,
автор: alenastarostenko74
Предмет: Обществознание,
автор: MarYndarYn