Question

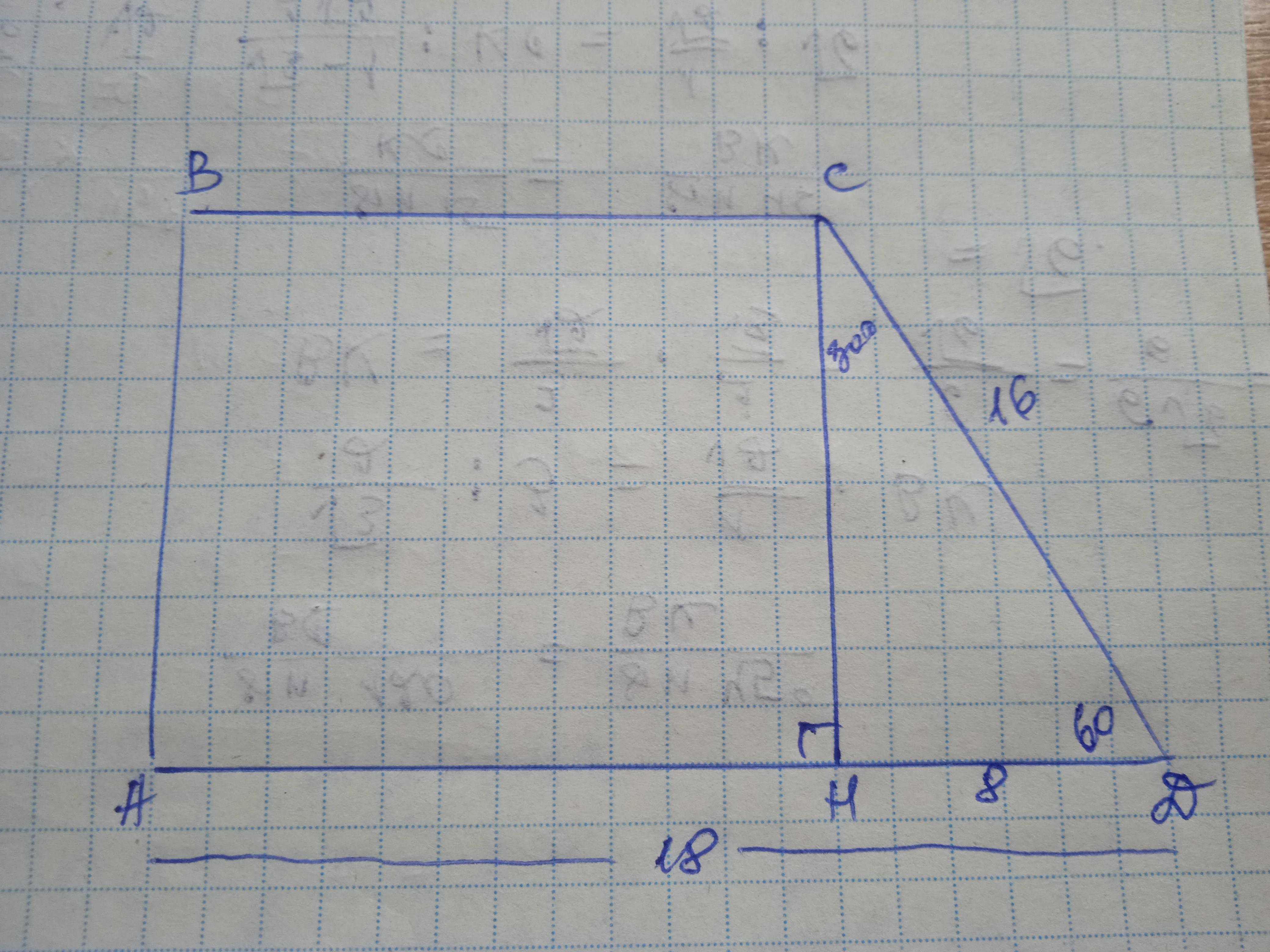
Задана прямоугольная трапеция ABCD. Большее основание AD = 18 см. Боковая сторона CD = 16 cм. Найдите площадь трапеции, если её острый угол равен 60°.

Answer 1

Ответ:

112√3 см²

Объяснение:

Дано: АВСD - трапеция,  АВ⊥АD,  АD=18 см,  СD=16 см,  ∠Д=60°. S(ABCD) - ?

Проведем высоту СН, рассмотрим ΔDСН - прямоугольный,  ∠DСН=90-60=30° по свойству суммы острых углов прямоугольного треугольника, значит DН=1/2 СD=16:2=8 см

По теореме Пифагора СН=√(СD²-DН²)=√(256-64)=√192=8√3 см.

ВС=АН=18-8=10 см.

S(ABCD)=(10+18):2*8√3=112√3 см²