Предмет: Геометрия,
автор: Аноним
Геометрия , очень срочно, помогите, дам лучший ответ
Приложения:
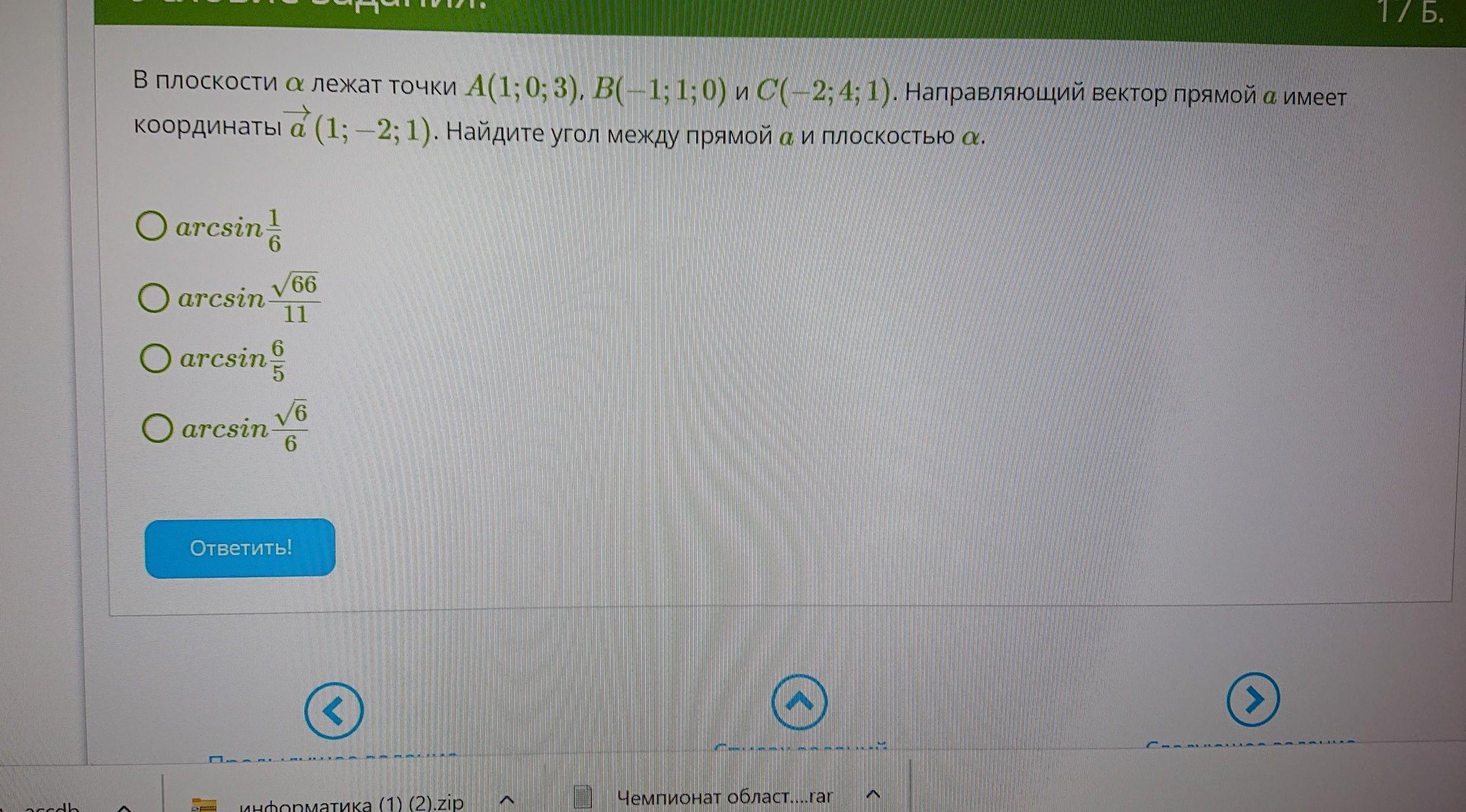
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Так как векторы и
лежат в этой плоскости, то вектор, равный их векторному произведению перпендикулярен этой плоскости и может служить вектором нормали.
Если точки и
— начало и конец вектора, то
Значит
Тогда
Через скалярное произведение найдем косинус угла между вектором нормали и вектором
тогда
Так как угол между плоскостью и ее нормалью прямой, то найденный угол отличается от искомого на
По формуле находим, что
Похожие вопросы
Предмет: Английский язык,
автор: danil641
Предмет: Окружающий мир,
автор: YuliaAy2011
Предмет: Английский язык,
автор: япосшпщтд
Предмет: Физика,
автор: emomnazarov03
Предмет: Математика,
автор: leha150304