Предмет: Математика,
автор: tiffany9888
Log5 64/(log5 48-log 5 3)
Ответы
Автор ответа:
0
Ответ:
Применяем свойства логарифмов:
Автор ответа:
0
Вітаю.
Відповідь: 1,5
Покрокове пояснення: фото
Приложения:
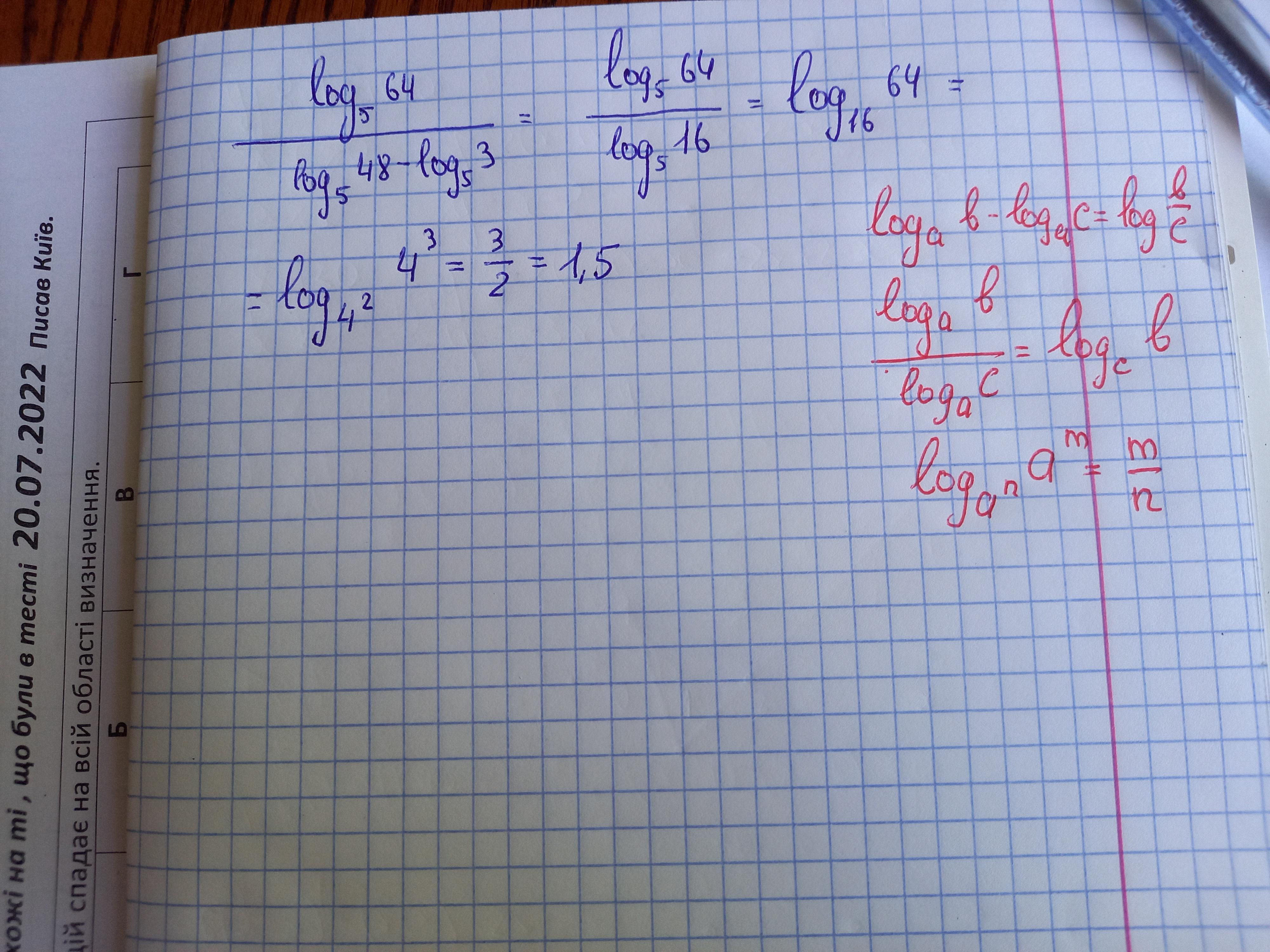
Похожие вопросы
Предмет: Українська мова,
автор: 54400htc
Предмет: Русский язык,
автор: ЛизаНаумкина
Предмет: Русский язык,
автор: annyu0108ta
Предмет: Русский язык,
автор: kseniamach6002
Предмет: История,
автор: lerika1105