НУЖНО СЕГОДНЯ ПОЖАЛУЙСТА
Дано куб ABCDA1B1C1D1, ребро якого дорівнює 1. Точки М і К є серединами
ребер АD і СD відповідно. Побудуйте переріз цього кубу, який проходить
через точки М, К і B1, та з’ясуйте, якою геометричною фігурою є цей переріз
(довести). Знайдіть його площу S.

Ответы
Ответ:
Cечение куба, проходящее через точки М, К и B1, является пятиугольником, его площадь S=7√17/24≈1.2026.
Объяснение:
Дано куб ABCDA1B1C1D1, ребро которого равно 1. Точки М и К являются серединами ребер АD и СD соответственно. Постройте сечение этого куба, проходящего через точки М, К и B1, и выясните, какой геометрической фигурой является это сечение (доказать). Найдите его площадь S.
-------
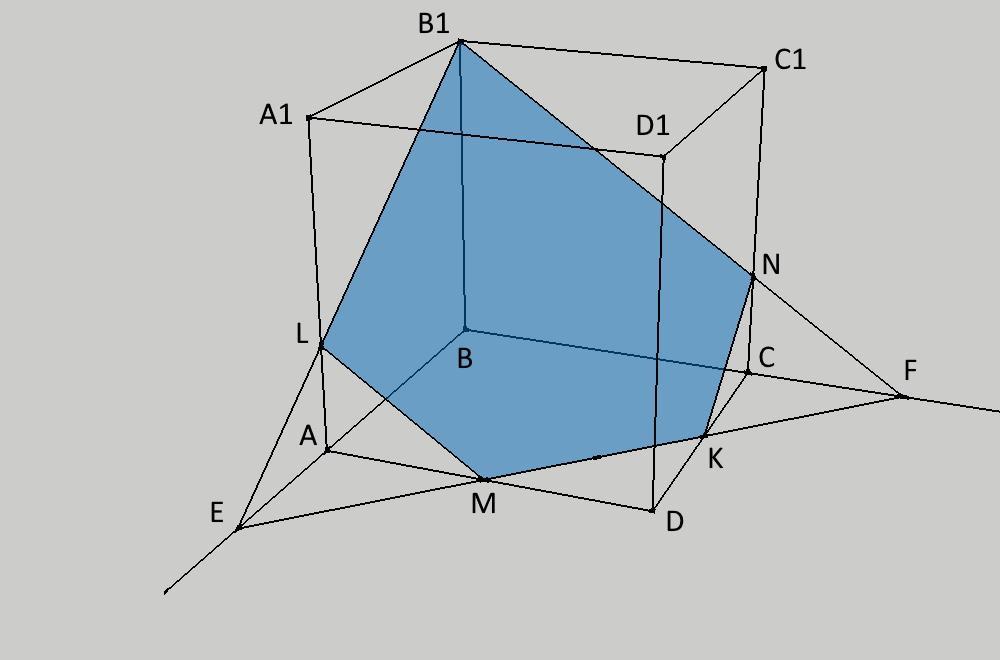
1. Построение сечения (приложение 1)
Проведем прямую MK и продолжим прямые BA и BC до пересечения с ней. Получим точки E и F соответственно, которые принадлежат плоскости будущего сечения.
Проведем прямы из вершины B1 к точкам E и F, они пересекут ребра AA1 и CC1 в точках в точках L и N соответственно. Точки L и N также принадлежат плоскости будущего сечения.
Соединим L с M и N с K - получим сечение B1NKML, который является пятиугольником.
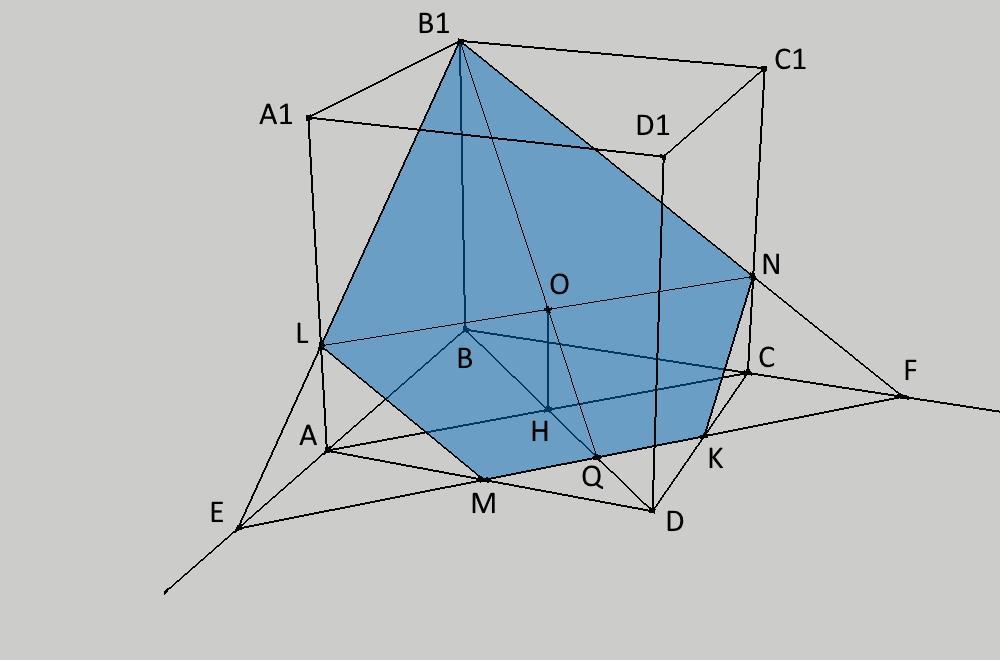
2. Вычисление площади (приложение 2)
Чтобы вычислить его площадь, проведем дополнительные построения.
Проведем прямую BD, она пересечет прямую MK в точке Q, проведем прямую B1Q и прямую LN, они пересекутся в точке O.
Из точки O проведем перпендикуляр к основанию куба OH. Точка H - пересечение диагоналей основания куба.
Отрезок LN разделил сечение на две фигуры: треугольник B1LN и четырехугольник LNKM.
Все построения симметричны относительно плоскости B1QB, поэтому треугольник B1LN - равнобедренный B1L=B1N, а B1O является его высотой.
AL=CN и перпендикулярны плоскости основания куба ABCD, а значит LN параллельна плоскости этого основания и в частности параллельна прямой MK. Четырехугольник LNKM является равнобедренной трапецией LM=NK.
LN=AC=√(AB²+BC²) = √2
MK является средней линией треугольника ACD и равна половине AC: MK = AC/2 = √2/2, а также делит его высоту DH на равные части: DQ=QH.
Тогда BQ = BH+HQ = √2/2+√2/4 = 3√2/4
B1Q = √(BB1²+BQ²) = √(1+(3√2/4)²) = √(8/8+9/8) = √(17/8) = √34/4
Треугольники BB1Q и HOQ подобны по двум углам, поэтому составим пропорцию:
B1Q:OQ = BQ:HQ = 3√2/4:√2/4 = 3
OQ = B1Q:3 = √34/4:3 = √34/12
B1O = B1Q-OQ = √34/4-√34/12 = 2√34/12 = √34/6
Теперь есть все данные, чтобы посчитать площадь сечения:
SΔB1LN = LN*B1O/2 = (√2*√34/6)/2 = √17/6
S(LNKM) = (LN+MK)*OQ/2 = (√2+√2/2)*(√34/12)/2 = (3√2/2)*√34/24 = √2*√34/16 = 2*√17/16 = √17/8
S(B1NKML) = √17/6+√17/8 = (4√17+3√17)/24 = 7√17/24 ≈ 1.2026
3. Вычисление площади (вариант)
Площадь ортогональной проекции выпуклого многоугольника на плоскость равна площади проецируемого многоугольника, умноженной на косинус угла между плоскостями многоугольника и его проекции:
S(MABCK) = S(B1NKML)*cos(∠B1QB)
Отсюда:
S(B1NKML) = S(MABCK)/cos(∠B1QB)
Площадь проекции равна площади основания за вычетом треугольника MKD:
S(MABCK) = S(ABCD)-S(MKD) = 1-(1/2)*(1/2)/2 = 1-1/8 = 7/8
Треугольник B1QB прямоугольный, поэтому косинус ∠B1QB - это отношение прилежащей стороны BQ к диагонали B1Q:
cos(∠B1QB) = BQ/B1Q = (3√2/4)/(√34/4) = 3/√17
Подставляем:
S(B1NKML) = (7/8)/(3/√17) = 7√17/24 ≈ 1.2026
#SPJ5