Question

НУЖНО СЕГОДНЯ СРОЧНО ПОЖАЛУЙСТА
У правильній трикутній піраміді двогранний кут при основі дорівнює

Answer 1

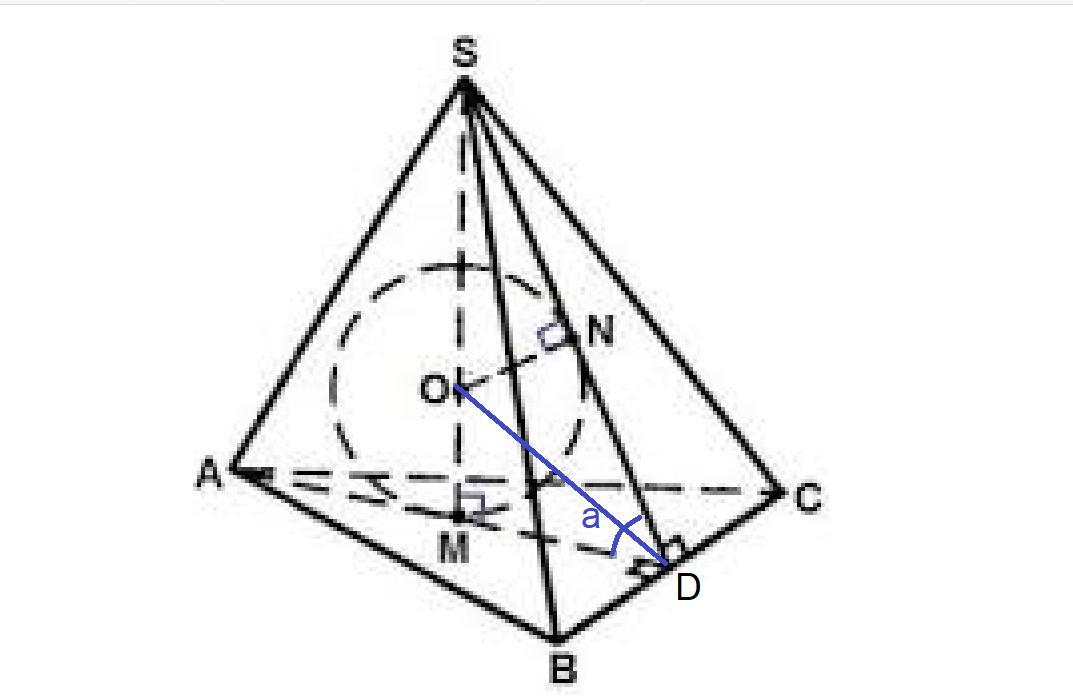
Находим отрезок MD: MD = OM/tg(a) = r/tg(a/2).

Для правильной треугольной пирамиды высота основания AD = 3MD.

h = AD = 3r/tg(a/2).

Отсюда находим ребро основания: a = AD/cos30° = (3r/tg(a/2)/(√3/2) = (√3r/(2tg(a/2)).

Тогда площадь основания So = a²√3/4 =  (3r²/(4tg²(a/2))*(√3/4) =

= (3√3r²/16tg²(a/2)).

Площадь боковой поверхности Sбок = So/cos(a) = (3√3r²/16tg²(a/2))/cos(a) = (3√3r²/16sin²(a/2))*cos(a)).

Получаем ответ: площадь полной поверхности равна S = So + Sбок =

= So + So/cos(a) = So(1 + (1/cos(a)) = (3√3r²/16tg²(a/2))* (1 + (1/cos(a)).