Предмет: Математика,
автор: clubanonim193
Даю 100 баллов. Решить уравнения:

pumpipop:
правильно ли вы написали первый пример?
да
Ответы
Автор ответа:
2
Ответ:
1) x₁ = 8 , x₂ = -3
2) x₁ = 4 , x₂ = -2
Пошаговое объяснение:
Решите уравнения :
1) ( x² - 5x - 23 )² - 2x² +* 10x + 47 = 0
2) ( x² - 2x )² - ( x - 1 )² = 55
1.
Если решать графически уравнение ( x² - 5x - 23 )² - 2x² - 10x + 47 = 0 , то по графику видно что нет пересечений с осью Ox , а значит действительных корней нет
Поэтому я считаю , что условие скорее всего должно было быть таким :
Сделаем замену
Тогда
Выходит полный квадрат
Вернемся к старой переменной
2.
Сделаем замену
Выходит биквадратное уравнение
Тогда
Вернемся к старой переменой t = x-1
Приложения:
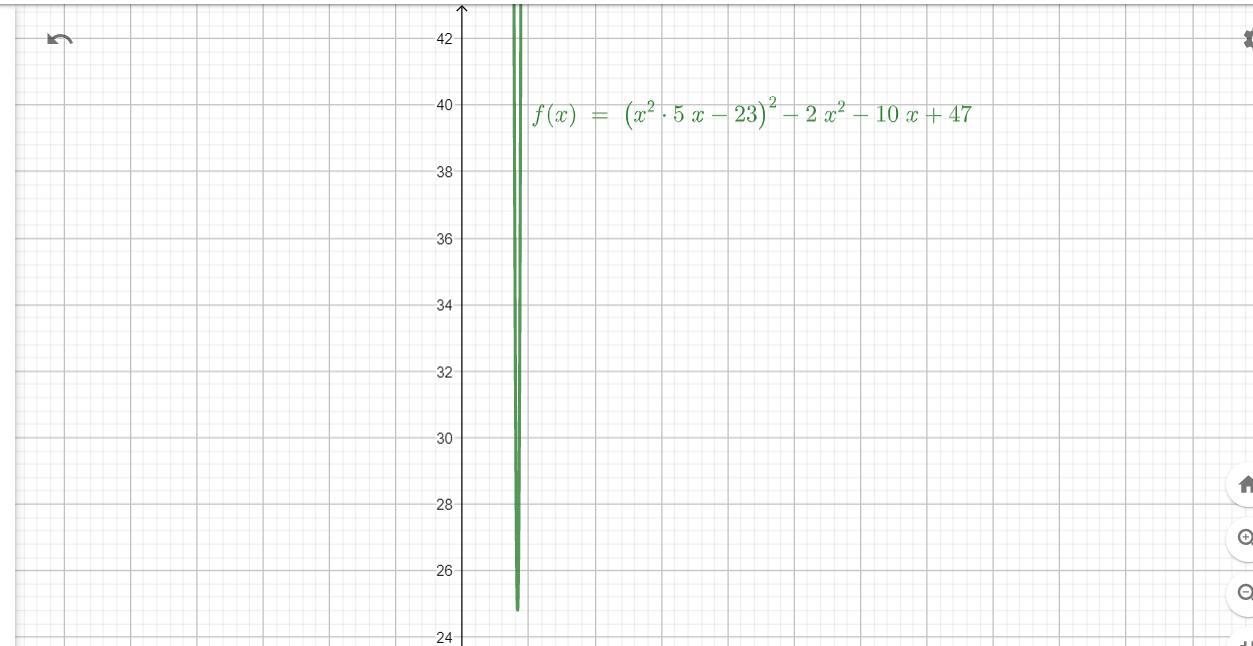
Изменил условие потому что оно скорее всего и должно было быть таким , по графику видно что нет пересечений с осью Ox , а значит действительных корней нет . Смотря на второе уравнение которое имеет действительные корни , я и сделал такой вывод .
понятно, спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: danilkazhuk
Предмет: Другие предметы,
автор: ЯнаПахомова
Предмет: Окружающий мир,
автор: ahmethanovalara888
Предмет: История,
автор: nastyakyper