Question

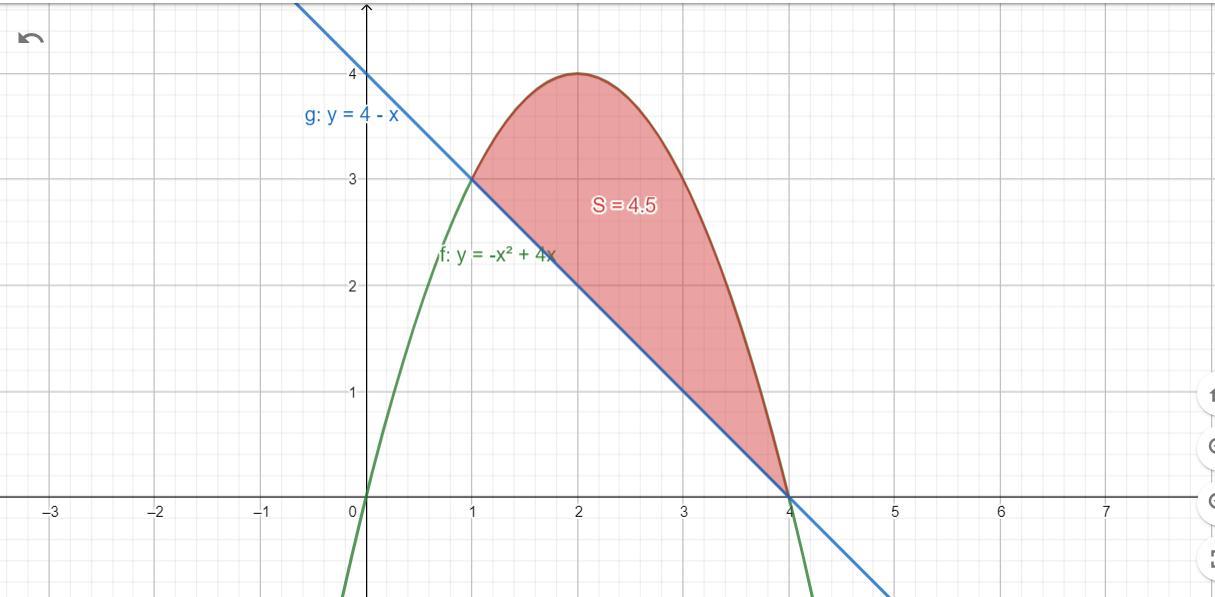
Вычислите площадь фигуры ограниченной линиями y=-x^2+4x и y=4-x

Answer 1

Ответ:

Площадь фигуры которая ограниченна линиями

y= -x² +4x и  y=4 -x равна 4,5 (ед)²

Объяснение:

Вычислите площадь фигуры ограниченной линиями

y=-x² +4x и  y=4 -x

Найдем точки пересечения данных графиков

$-x ^2 +4x = 4 - x \\\\ x^2 -5x + 4=0 \\\\ (x -4)(x-1) = 0 \\\\ x_1 = 4 ~~ ; ~~ x_2 = 1$

Из промежутка  (1  ; 4 ) возьмем любую число   и подставим в каждую функцию ,   пусть это будет x = 2

1) y = -x² +4x
  y  = -4 + 8 = 4

2) y = 4 - x
    y  = 4 -2 = 2

Видно что первая  функция  в данном промежутке  больше второй  ,  поэтому при нахождении площади  от  первой  функции отнимем  вторую

Находим площадь

$\displaystyle \int\limits^4_1( -x^2 +4x - (4-x) )\, dx = \int\limits^4_1( -x^2 +5x -4 )\, dx= \Big ( -\frac{x^3}{3} + \frac{5x^2}{2} -4x \Big ) \Bigg |^4_1 = \\\\\\ -\frac{64}{3} + 40 - 16 - \bigg ( -\frac{1}{3} + 2,5 - 4 \bigg ) = \frac{-64+1}{3} + 24 +1,5 = \\\\\\\ = 25,5 -21 = 4,5$



#SPJ1